Newton's Universal Law of Gravitation

Newton's universal law of gravitation states that every particle in the universe attracts every other particle with a force along a line joining them. The force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. For two bodies having masses $m$ and $M$ with a distance $r$ between their centers of mass, the equation for Newton's universal law of gravitation is:

$\displaystyle F = G\frac{mM}{r^2}$

The gravitational force is responsible for artificial satellites orbiting the Earth. The Moon's orbit about Earth, the orbits of planets, asteroids, meteors, and comets about the Sun are other examples of gravitational orbits. Historically, Kepler discovered his 3 laws (called Kepler's law of planetary motion) long before the days of Newton. Kepler devised his laws after careful study (over some 20 years) of a large amount of meticulously recorded observations of planetary motion done by Tycho Brahe (1546–1601).

Kepler's Laws

• The orbit of each planet about the Sun is an ellipse with the Sun at one focus.
• Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal times.
• The ratio of the squares of the periods of any two planets about the Sun is equal to the ratio of the cubes of their average distances from the Sun.

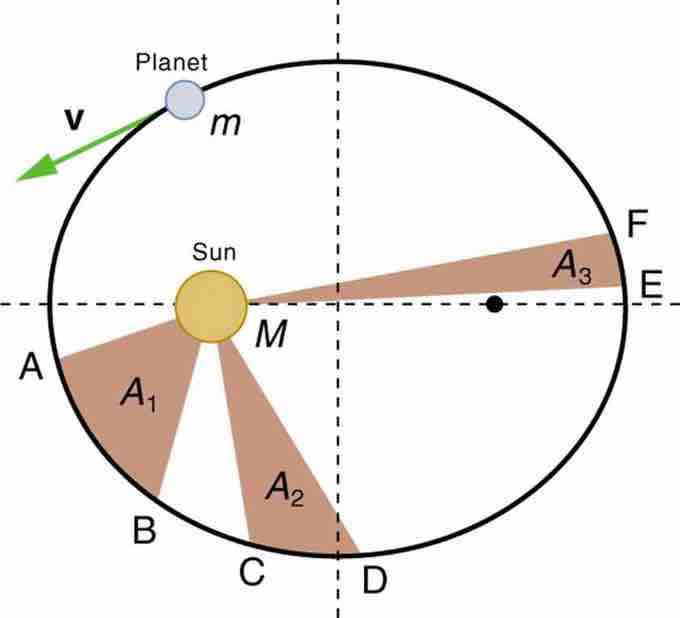
Kepler's Second Law

The shaded regions have equal areas. It takes equal times for $m$ to go from $A$ to $B$, from $C$ to $D$, and from $E$ to $F$. The mass $m$ moves fastest when it is closest to $M$. Kepler's second law was originally devised for planets orbiting the Sun, but it has broader validity.

Ellipses and Kepler's First Law

(a) An ellipse is a closed curve such that the sum of the distances from a point on the curve to the two foci ($f_1$ and $f_2$) is a constant. You can draw an ellipse as shown by putting a pin at each focus, and then placing a string around a pencil and the pins and tracing a line on paper. A circle is a special case of an ellipse in which the two foci coincide (thus any point on the circle is the same distance from the center). (b) For any closed gravitational orbit, $m$ follows an elliptical path with $M$ at one focus. Kepler's first law states this fact for planets orbiting the Sun.

Derivation of Kepler's Third Law For Circular Orbits

Kepler's 3rd law is equivalent to: 

$\displaystyle \frac{T_1^2}{T_2^2} = \frac{r_1^3}{r_2^3}$ 

$T$ is the period (time for one orbit) and $r$ is the average radius. We shall derive Kepler's third law, starting with Newton's laws of motion and his universal law of gravitation. We will assume a circular path (not an elliptical one) for simplicity.

Let us consider a circular orbit of a small mass $m$ around a large mass $M$, satisfying the two conditions stated at the beginning of this section. Gravity supplies the centripetal force to mass $m$. Therefore, for a uniform circular motion:

 $\displaystyle G\frac{mM}{r^2} = ma_c = m\frac{v^2}{r}$

The mass $m$ cancels, yielding: 

$\displaystyle G\frac{M}{r} = v^2$

Now, to get at Kepler's third law, we must get the period $T$ into the equation. By definition, period $T$ is the time for one complete orbit. Now the average speed $v$ is the circumference divided by the period:

$\displaystyle v = \frac{2\pi r }{T} $ 

Substituting this into the previous equation gives: 

$\displaystyle G\frac{M}{r} = \frac{4 \pi ^2 r^2}{T^2}$ 

Solving for $T^2$ yields:

$\displaystyle T^2 = \frac{4\pi^2}{GM} r^3$ 

Since $T^2$ is proportional to $r^3$, their ratio is constant. This is Kepler's 3rd law.