Overview

As an example of a uniform circular motion and its application, let us now consider banked curves, where the slope of the road helps you negotiate the curve. The greater the angle $\theta$, the faster you can take the curve. Race tracks for bikes as well as cars, for example, often have steeply banked curves. In an "ideally banked curve," the angle $\theta$ is such that you can negotiate the curve at a certain speed without the aid of friction between the tires and the road. We will derive an expression for $\theta$ for an ideally banked curve for speed $v$ and consider an example related to it.

Uniform Circular Motion and Determining Ideal Banking Conditions

For ideal banking, the net external force equals the horizontal centripetal force in the absence of friction. The components of the normal force $N$ in the horizontal and vertical directions must equal the centripetal force and the weight of the car, respectively. In cases in which forces are not parallel, it is most convenient to consider components along perpendicular axes—in this case, the vertical and horizontal directions.

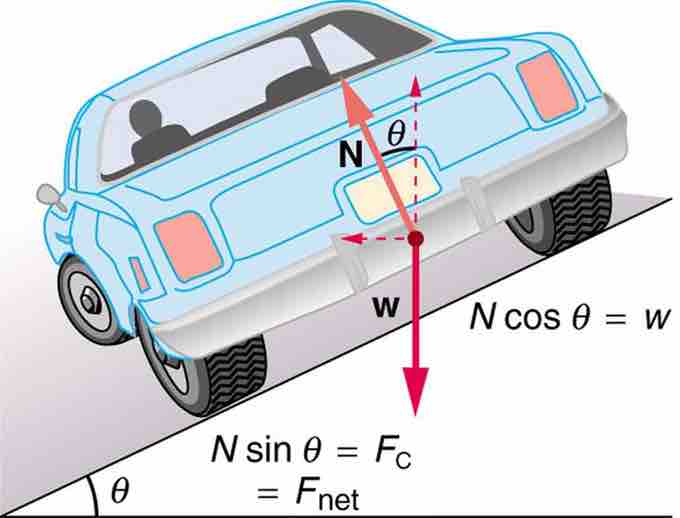
Car on a Banked Curve

The car on this banked curve is moving away and turning to the left.

Above is a free body diagram for a car on a frictionless banked curve. The only two external forces acting on the car are its weight $w$ and the normal force of the road $N$. (A frictionless surface can only exert a force perpendicular to the surface—that is, a normal force. ) These two forces must add to give a net external force that is horizontal toward the center of curvature and has magnitude $\frac{mv^2}{r}$. Only the normal force has a horizontal component, and so this must equal the centripetal force—that is:

$\displaystyle N\sin\theta = \frac {mv^2}{r}$ 

Because the car does not leave the surface of the road, the net vertical force must be zero, meaning that the vertical components of the two external forces must be equal in magnitude and opposite in direction. From the figure, we see that the vertical component of the normal force is $N\cos\theta$, and the only other vertical force is the car's weight. These must be equal in magnitude, thus:

$N\cos\theta = mg$ 

Dividing the above equations yields:

$\displaystyle \tan \theta = \frac{v^2}{rg}$ 

Taking the inverse tangent gives:

$\displaystyle \theta = \tan^{-1}(\frac{v^2}{rg})$

for an ideally banked curve with no friction.

This expression can be understood by considering how $\theta$ depends on $v$ and $r$. A large $\theta$ will be obtained for a large $v$ and a small $r$. That is, roads must be steeply banked for high speeds and sharp curves. Friction helps, because it allows you to take the curve at greater or lower speed than if the curve is frictionless. Note that $\theta$ does not depend on the mass of the vehicle.