Projectile motion is a form of motion where an object moves in a parabolic path. The path followed by the object is called its trajectory. Projectile motion occurs when a force is applied at the beginning of the trajectory for the launch (after this the projectile is subject only to the gravity).
One of the key components of the projectile motion, and the trajectory it follows, is the initial launch angle. The angle at which the object is launched dictates the range, height, and time of flight the object will experience while in projectile motion. shows different paths for the same object being launched at the same initial velocity and different launch angles. As illustrated by the figure, the larger the initial launch angle and maximum height, the longer the flight time of the object.
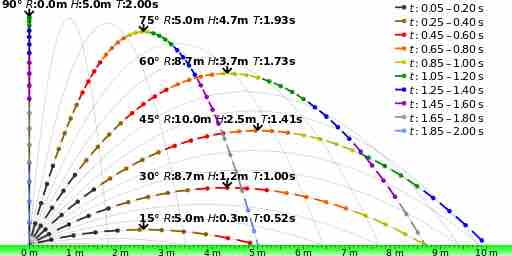
Projectile Trajectories
The launch angle determines the range and maximum height that an object will experience after being launched.This image shows that path of the same object being launched at the same speed but different angles.
We have previously discussed the effects of different launch angles on range, height, and time of flight. However, what happens if there is no angle, and the object is just launched horizontally? It makes sense that the object should be launched at a certain height (
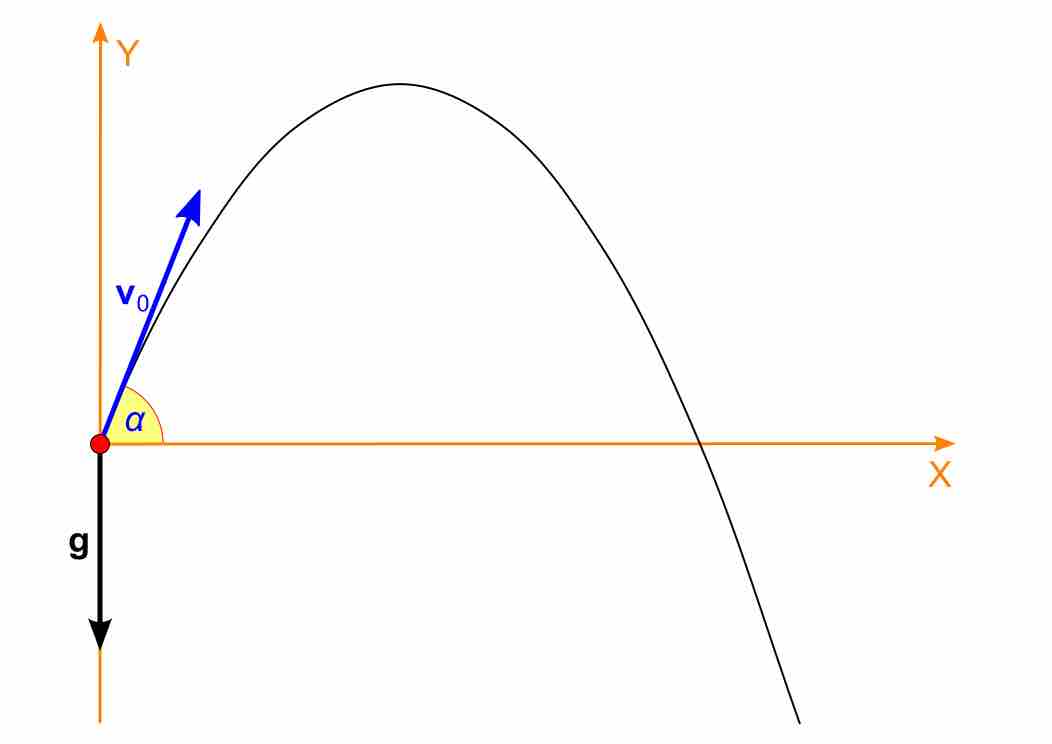
Projectile motion
Projectile moving following a parabola.Initial launch angle is
Duration of Flight
There is no vertical component in the initial velocity (
Here,
Range
In the horizontal direction, the object travels at a constant speed