Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning of the trajectory, after which the only interference is from gravity.
One of the key components of projectile motion and the trajectory that it follows is the initial launch angle. This angle can be anywhere from 0 to 90 degrees. The angle at which the object is launched dictates the range, height, and time of flight it will experience while in projectile motion. shows different paths for the same object launched at the same initial velocity at different launch angles. As you can see from the figure, the larger the initial launch angle, the closer the object comes to maximum height and the longer the flight time. The largest range will be experienced at a launch angle up to 45 degrees.
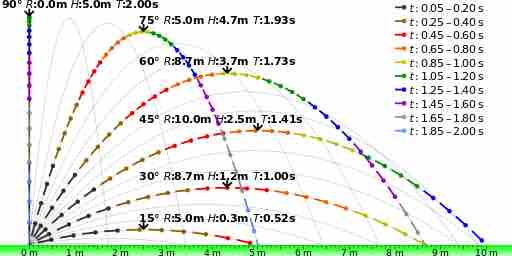
Launch Angle
The launch angle determines the range and maximum height that an object will experience after being launched. This image shows that path of the same object being launched at the same velocity but different angles.
The range, maximum height, and time of flight can be found if you know the initial launch angle and velocity, using the following equations:
Where R - Range, h - maximum height, T - time of flight, vi - initial velocity, θi - initial launch angle, g - gravity.
Now that we understand how the launch angle plays a major role in many other components of the trajectory of an object in projectile motion, we can apply that knowledge to making an object land where we want it. If there is a certain distance, d, that you want your object to go and you know the initial velocity at which it will be launched, the initial launch angle required to get it that distance is called the angle of reach. It can be found using the following equation: