Projectile Motion
Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning on the trajectory, after which the only interference is from gravity. In a previous atom we discussed what the various components of an object in projectile motion are. In this atom we will discuss the basic equations that go along with them in the special case in which the projectile initial positions are null (i.e.
Initial Velocity
The initial velocity can be expressed as x components and y components:
In this equation,
Time of Flight
The time of flight of a projectile motion is the time from when the object is projected to the time it reaches the surface. As we discussed previously,
Acceleration
In projectile motion, there is no acceleration in the horizontal direction. The acceleration,
Velocity
The horizontal velocity remains constant, but the vertical velocity varies linearly, because the acceleration is constant. At any time,
You can also use the Pythagorean Theorem to find velocity:
Displacement
At time, t, the displacement components are:
The equation for the magnitude of the displacement is
Parabolic Trajectory
We can use the displacement equations in the x and y direction to obtain an equation for the parabolic form of a projectile motion:
Maximum Height
The maximum height is reached when
where
Range
The range of the motion is fixed by the condition
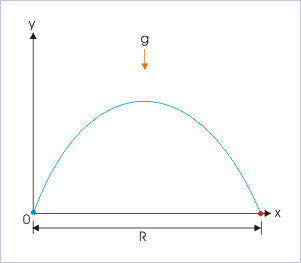
Range of Trajectory
The range of a trajectory is shown in this figure.