Isothermal Processes

An isothermal process is a change of a system, in which the temperature remains constant: ΔT = 0. This typically occurs when a system is in contact with an outside thermal reservoir (heat bath), and the change occurs slowly enough to allow the system to continually adjust to the temperature of the reservoir through heat exchange. In contrast, an adiabatic process is where a system exchanges no heat with its surroundings (Q = 0). (See our atom on "Adiabatic Process. ") In other words, in an isothermal process, the value ΔT = 0 but Q ≠ 0, while in an adiabatic process, ΔT ≠ 0 but Q = 0.

Ideal Gas in an Isothermal Process

For an ideal, the product of pressure and volume (PV) is a constant if the gas is kept at isothermal conditions. (This is historically called Boyle's law. ) However, the cases where the product PV is an exponential term, does not comply. The value of the constant is nRT, where n is the number of moles of gas present and R is the ideal gas constant. In other words, the ideal gas law PV = nRT applies. This means that

$P = \frac{nRT}{V} = \frac{constant}{V}$

holds.

Calculation of Work

In thermodynamics, the work involved when a gas changes from state A to state B is simply

$W_{A\to B} = \int_{V_A}^{V_B}P\,dV$.

For an isothermal, reversible process, this integral equals the area under the relevant pressure-volume isotherm, and is indicated in blue in for an ideal gas. Again, P = nRT / V applies and with T being constant (as this is an isothermal process), we have

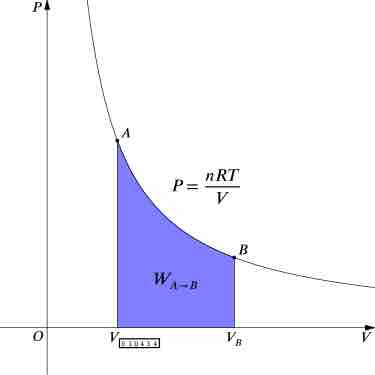
Work Done by Gas During Expansion

The blue area represents "work" done by the gas during expansion for this isothermal change.

$W_{A\to B} = nRT\int_{V_A}^{V_B}\frac{1}{V}dV = nRT\ln{\frac{V_B}{V_A}}$.

It is also worth noting that, for many systems, if the temperature is held constant, the internal energy of the system also is constant, and so $\Delta U = 0$. From the first law of thermodynamics, it follows that $Q =-W$ for this same isothermal process.