We now move from consideration of forces that affect the motion of an object (such as friction and drag) to those that affect an object's shape. If a bulldozer pushes a car into a wall, the car will not move past the wall but it will noticeably change shape. A change in shape due to the application of a force is a deformation. Even very small forces are known to cause some deformation. For small deformations, two important characteristics are observed. First, the object returns to its original shape when the force is removed—that is, the deformation is elastic for small deformations. Second, the size of the deformation is proportional to the force—that is, for small deformations, Hooke's law is obeyed. In equation form, Hooke's law is given by
Deformations come in several types: changes in length (tension and compression), sideways shear (stress), and changes in volume.
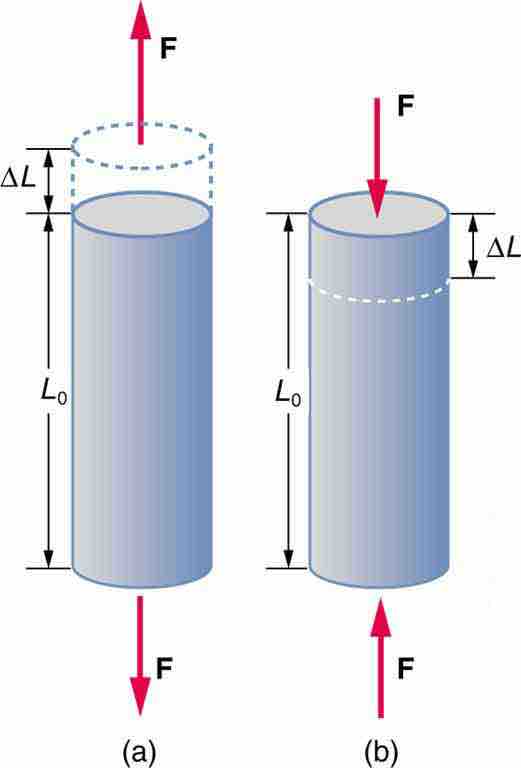
Tension/Compression
Tension: The rod is stretched a length
The ratio of force to area
Stress and strain are related to each other by a constant called Young's Modulus or the elastic modulus which varies depending on the material. Using Young's Modulus the relation between stress and strain is given by:
A material with a high elastic modulus is said to have high tensile strength. Such materials are very resistant to being stretched and require a large amount of force to deform a small amount.