Speed Distribution of Molecules

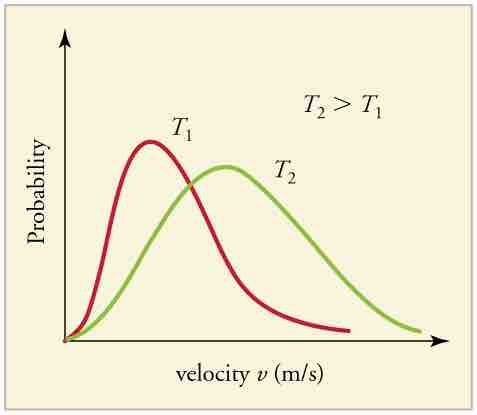
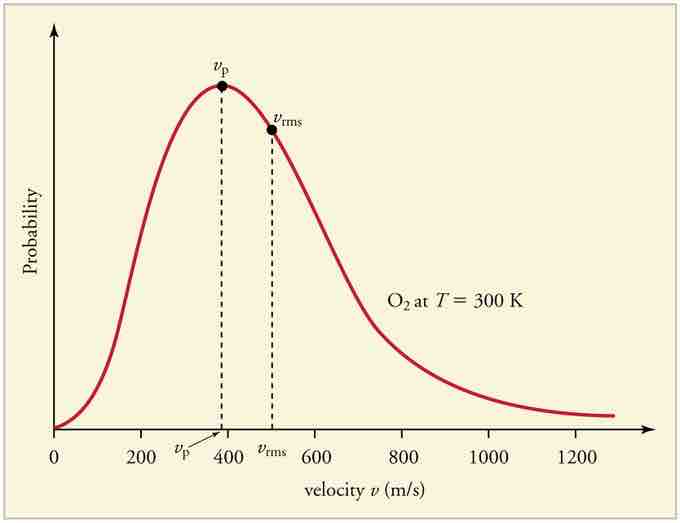
The motion of molecules in a gas is random in magnitude and direction for individual molecules, but a gas of many molecules has a predictable distribution of molecular speeds, known as the Maxwell-Boltzmann distribution (illustrated in ). The distribution has a long tail because some molecules may go several times the rms speed. The most probable speed v_p (at the peak of the curve) is less than the rms speed v_rms. As shown in , the curve is shifted to higher speeds at higher temperatures, with a broader range of speeds.

Maxwell-Boltzmann Distribution at Higher Temperatures

The Maxwell-Boltzmann distribution is shifted to higher speeds and is broadened at higher temperatures.

Maxwell-Boltzmann Distribution

The Maxwell-Boltzmann distribution of molecular speeds in an ideal gas. The most likely speed v_p is less than the rms speed v_rms. Although very high speeds are possible, only a tiny fraction of the molecules have speeds that are an order of magnitude greater than v_rms.

Maxwell-Boltzmann Distribution

Maxwell-Boltzmann distribution is a probability distribution. It applies to ideal gases close to thermodynamic equilibrium, and is given as the following equation:

$f_\mathbf{v} (v_x, v_y, v_z) = \left(\frac{m}{2 \pi kT} \right)^{3/2} \exp \left[- \frac{m(v_x^2 + v_y^2 + v_z^2)}{2kT} \right]$,

where fv is the velocity probability density function. (Derivation of the formula goes beyond the scope of introductory physics. ) The formula calculates the probability of finding a particle with velocity in the infinitesimal element [dv_x, dv_y, dv_z] about velocity v = [v_x, v_y, v_z] is:

$f_\mathbf{v} \left(v_x, v_y, v_z\right)\, dv_x\, dv_y\, dv_z$.

It can also be shown that the Maxwell–Boltzmann velocity distribution for the vector velocity [v_x, v_y, v_z] is the product of the distributions for each of the three directions:

$f_v \left(v_x, v_y, v_z\right) = f_v (v_x)f_v (v_y)f_v (v_z)$,

where the distribution for a single direction is,

$f_v (v_i) = \sqrt{\frac{m}{2 \pi kT}} \exp \left[ \frac{-mv_i^2}{2kT} \right]$.

This makes sense because particles are moving randomly, meaning that each component of the velocity should be independent.

Distribution for the Speed

Usually, we are more interested in the speeds of molecules rather than their component velocities. The Maxwell–Boltzmann distribution for the speed follows immediately from the distribution of the velocity vector, above. Note that the speed is:

$v = \sqrt{v_x^2 + v_y^2 + v_z^2}$

and the increment of volume is:

$dv_x\, dv_y\, dv_z = v^2 \sin \phi\, dv\, d\theta\, d\phi$,

where $\theta$ and $\phi$ are the "course" (azimuth of the velocity vector) and "path angle" (elevation angle of the velocity vector). Integration of the normal probability density function of the velocity, above, over the course (from 0 to $2\pi$) and path angle (from 0 to $\pi$), with substitution of the speed for the sum of the squares of the vector components, yields the following probability density function (known simply as the Maxwell distribution):

$f(v) = \sqrt{\left(\frac{m}{2 \pi kT}\right)^3}\, 4\pi v^2 \exp \left(\frac{-mv^2}{2kT}\right)$ for speed v.