Overview of Intensity
Sound Intensity is the power per unit area carried by a wave . Power is the rate that energy is transferred by a wave.
The equation used to calculate this intensity, I, is:
Sound Intensity
Sound intensity can be found from the following equation:
Sound Intensity
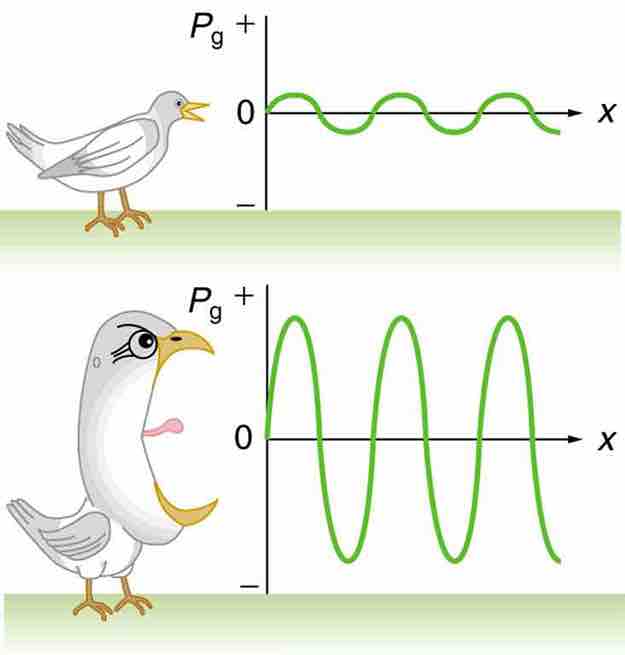
Graphs of the gauge pressures in two sound waves of different intensities. The more intense sound is produced by a source that has larger-amplitude oscillations and has greater pressure maxima and minima. Because pressures are higher in the greater-intensity sound, it can exert larger forces on the objects it encounters
Although the units for sound intensity are technically watts per meter squared, it is much more common for it to be referred to as decibels, dB. A decibel is a ratio of the observed amplitude, or intensity level to a reference, which is 0 dB. The equation for this is:
For a reference point on intensity levels, below are a list of a few different intensities: