Sound can be produced in many ways, by many different instruments and devices. A vibrating string or air column can both make interesting music and it is good to understand the physics behind both.
Vibrating Strings
There are many instruments that produce sound based on strings. Guitars, cellos, pianos and many other examples. These sounds are produced by standing waves in the strings. These waves and their frequencies are constant, and therefor the sound and pitch produced by them is constant. This figure shows a visual of a standing wave in a string: The speed of the wave is proportional to the root of the string tension, and inversely proportional to the root of the string density, shown by the following equation:
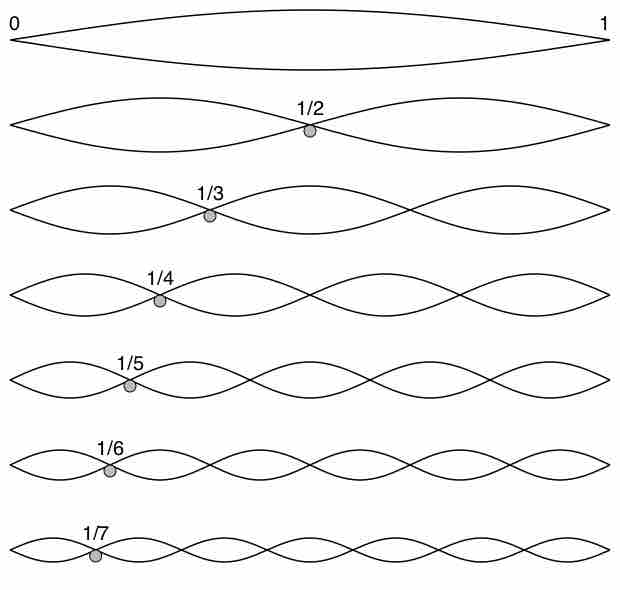
Standing Waves in a String
Vibration, standing waves in a string. The fundamental and the first 6 overtones form a harmonic series.
Air Columns
Many instruments make music by causing a vibration to a column of air in a resonator. These are usually called wind instruments. Examples of these are flutes, recorders, and saxophones. They are either open at both ends, or closed at one end and open at the other. The pitch of the sound is a function of the frequency. There are many factors that go into finding the frequency. Lets start with the tubes that are closed at one end and open at the other.
Closed Air Tubes:The maximum displacement of the air occurs at the open end of the tube, and is called the antinode. The air movement is constrained at the closed end, and there is no displacement, and this is called the node. The distance from the node to the antinode is 1/4 the length of one wavelength, and equal to the length of the tube, as shown in this equation:
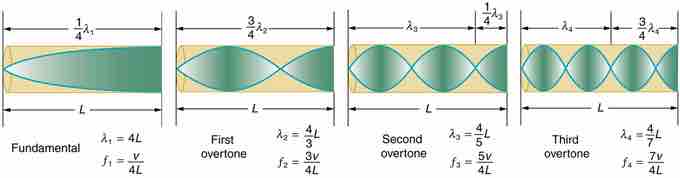
An Air column in a tube closed at one end
The fundamental and three lowest overtones for a tube closed at one end. All have maximum air displacements at the open end and none at the closed end.
Open Air tubes:Air tubes can also be open at both ends. They are very similar to the ones we talked about above, but there is an antinode at both ends, since they are both open, as shown in this figure: Since there is an antinode at both ends, we can see that the length of a wavelength is found by this equation: