Spherical Waves
Christiaan Huygens was a Dutch scientist who developed a useful technique for determining how and where waves propagate. In 1678, he proposed that every point that a luminous disturbance touches becomes itself a source of a spherical wave; the sum of these secondary waves determines the form of the wave at any subsequent time. The Huygen-Fresnel Principle shows that as the waves interact with each other, they interfere either constructively or destructively . Constructive interference occurs when waves are completely in phase with each other and amplifies the waves. Destructive interference occurs when waves are exactly out of phase with either other, and if waves are perfectly out of phase with each other, the wave will be canceled out completely. Since the waves all come from one point source, the waves happen in a spherical pattern. All the waves come from a single point source and are spherical .

Spherical Wave
When waves are produced from a point source, they are spherical waves.
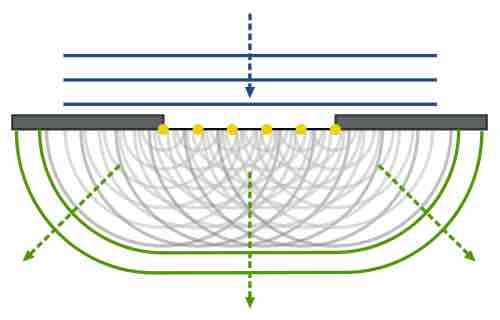
Huygen-Fresnel Principle
The Huygen-Fresnel Principle uses the law of refraction. Each point on the wave produces waves which interfere with each other either constructively or destructively.
Plane Waves
A plane wave is a constant-frequency wave whose wavefronts (surfaces of constant phase) are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector . It is not possible in practice to have a true plane wave; only a plane wave of infinite extent will propagate as a plane wave. However, many waves are approximately plane waves in a localized region of space. For example, a localized source such as an antenna produces a field that is approximately a plane wave far from the antenna in its far-field region. Similarly, if the length scales are much longer than the wave's wavelength, as is often the case for light in the field of optics, one can treat the waves as light rays which correspond locally to plane waves.
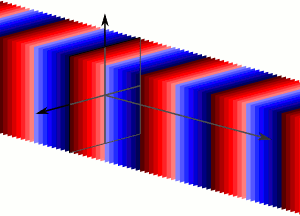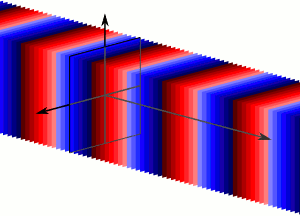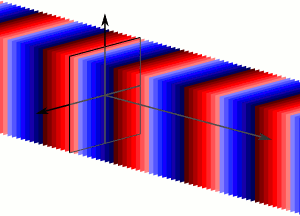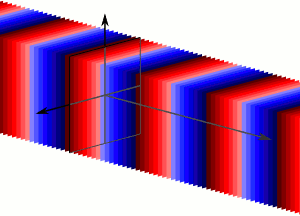
Plane Wave
Plane waves are an infinite number of wavefronts normal to the direction of the propogation.