Angular momentum and angular velocity have both magnitude and direction and, therefore, are vector quantities. The direction of these quantities is inherently difficult to track—a point on a rotating wheel is constantly rotating and changing direction. The axis of rotation of a rotating wheel is the only place that has a fixed direction. The direction of angular momentum and velocity can be determined along this axis.
Imagine the axis of rotation as a pole through the center of a wheel. The pole protrudes on both sides of the wheel and, depending on which side you're looking at, the wheel is turning either clockwise or counterclockwise. This dependency on perspective makes determining the angle of rotation slightly more difficult. As with all physical quantities, there is a standard for measurement that makes these types of quantities consistent. For angular quantities, the direction of the vector is determined using the Right Hand Rule, illustrated in .
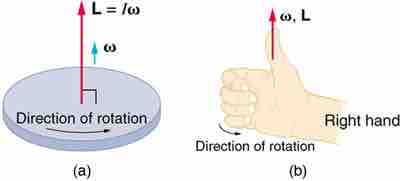
The Right Hand Rule
Figure (a) shows a disk is rotating counterclockwise when viewed from above. Figure (b) shows the right-hand rule. The direction of angular velocity ω size and angular momentum L are defined to be the direction in which the thumb of your right hand points when you curl your fingers in the direction of the disk's rotation as shown.
The right hand rule can be used to find the direction of both the angular momentum and the angular velocity. From a spinning disc, for example, let's again imagine a pole through the center of the disc, at the axis of rotation. Using the right hand rule, your right hand would be grasping the pole so that your four fingers (index, middle, ring, and pinky) are following the direction of rotation. That is, an imaginary arrow from your wrist to your fingertips points in the same direction as the disc is rotating. In addition, your thumb is pointing straight out in the axis, perpendicular to your other fingers (or parallel to the 'pole' at the axis of rotation). Using this right hand rule, the direction of angular velocity ω and angular momentum L are defined as the direction in which the thumb of your right hand points when you curl your fingers in the direction of the disc's rotation.