Magnitude of the Magnetic Force
How does one magnet attracts another? The answer relies on the fact that all magnetism relies on current, the flow of charge. Magnetic fields exert forces on moving charges, and so they exert forces on other magnets, all of which have moving charges.
The magnetic force on a moving charge is one of the most fundamental known. The magnetic force is as important as the electrostatic or Coulomb force. Yet the magnetic force is more complex, in both the number of factors that affects it and in its direction, than the relatively simple Coulomb force. The magnitude of the magnetic force
where θ is the angle between the directions of
Because sinθ is unitless, the tesla is
Another smaller unit, called the gauss (G), where 1 G=10−4 T, is sometimes used. The strongest permanent magnets have fields near 2 T; superconducting electromagnets may attain 10 T or more. The Earth's magnetic field on its surface is only about 5×10−5 T, or 0.5 G.
The direction of the magnetic force
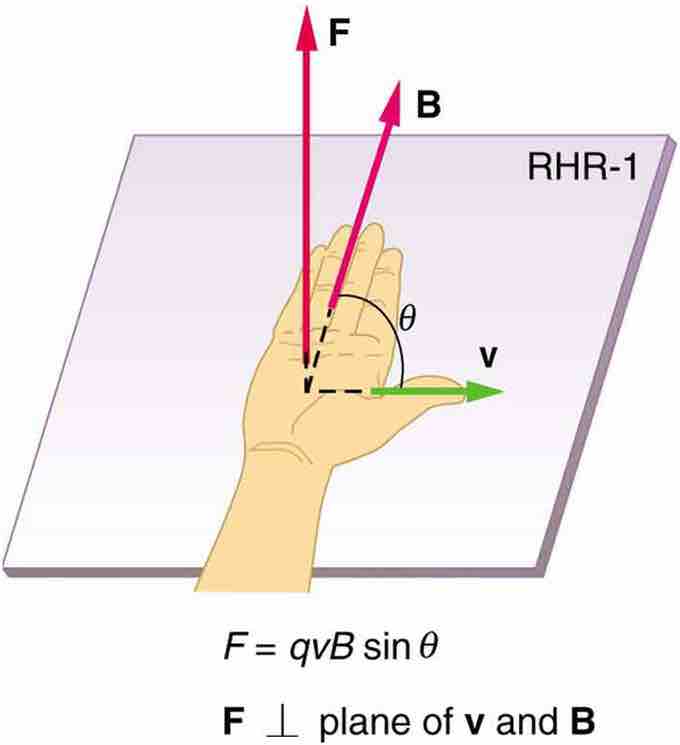
Right Hand Rule
Magnetic fields exert forces on moving charges. This force is one of the most basic known. The direction of the magnetic force on a moving charge is perpendicular to the plane formed by v and B and follows right hand rule–1 (RHR-1) as shown. The magnitude of the force is proportional to q, v, B, and the sine of the angle between v and B.