The Hall effect is the phenomenon in which a voltage difference (called the Hall voltage) is produced across an electrical conductor, transverse to the conductor's electric current when a magnetic field perpendicular to the conductor's current is applied.
When a magnetic field is present that is not parallel to the motion of moving charges within a conductor, the charges experience the Lorentz force. In the absence of such a field, the charges follow a roughly straight path, occasionally colliding with impurities.
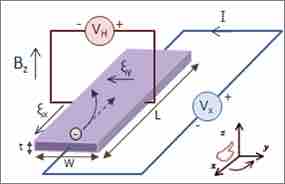
In the presence of a magnetic field with a perpendicular component, the paths charges take becomes curved such that they accumulate on one face of the material. On the other face, there is an excess of opposite charge remaining. Thus, an electric potential is created so long as the charge flows. This opposes the magnetic force, eventually to the point of cancelation, resulting in electron flow in a straight path .
Hall Effect for Electrons
Initially, the electrons are attracted by the magnetic force and follow the curved arrow. Eventually, when electrons accumulate in excess on the left side and are in deficit on the right, an electric field ξy is created. This force becomes strong enough to cancel out the magnetic force, so future electrons follow a straight (rather than curved) path.
For a metal containing only one type of charge carrier (electrons), the Hall voltage (VH) can be calculated as a factor of current (I), magnetic field (B), thickness of the conductor plate (t), and charge carrier density (n) of the carrier electrons:
In this formula, e represents the elementary charge.
The Hall coefficient (RH) is a characteristic of a conductor's material, and is defined as the ratio of induced electric field (Ey) to the product of current density (jx) and applied magnetic field (B):
The Hall effect is a rather ubiquitous phenomenon in physics, and appears not only in conductors, but semiconductors, ionized gases, and in quantum spin among other applications.