Reference Frames and Displacement

In order to describe an object's motion, you need to specify its position relative to a convenient reference frame.

Learning Objective

Evaluate displacement within a frame of reference.

Key Points

Choosing a frame of reference requires deciding where the object's initial position is and which direction will be considered positive.
Valid frames of reference can differ from each other by moving relative to one another.
Frames of reference are particularly important when describing an object's displacement.
Displacement is the change in position of an object relative to its reference frame.

Terms

frame of reference
A coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it.
displacement
A vector quantity that denotes distance with a directional component.

Full Text

In order to describe the motion of an object, you must first describe its position -- where it is at any particular time. More precisely, you need to specify its position relative to a convenient reference frame. Earth is often used as a reference frame, and we often describe the position of objects related to its position to or from Earth. Mathematically, the position of an object is generally represented by the variable x.

Frames of Reference

There are two choices you have to make in order to define a position variable x. You have to decide where to put x = 0 and which direction will be positive. This is referred to as choosing a coordinate system, or choosing a frame of reference. As long as you are consistent, any frame is equally valid. But you don't want to change coordinate systems in the middle of a calculation. Imagine sitting in a train in a station when suddenly you notice that the station is moving backward. Most people would say that they just failed to notice that the train was moving -- it only seemed like the station was moving. But this shows that there is a third arbitrary choice that goes into choosing a coordinate system: valid frames of reference can differ from each other by moving relative to one another. It might seem strange to use a coordinate system moving relative to the earth -- but, for instance, the frame of reference moving along with a train might be far more convenient for describing things happening inside the train. Frames of reference are particularly important when describing an object's displacement.

FRAMES OF REFERENCE by Professor Hume and Professor Donald Ivey of the University of Toronto

In this classic film, Professors Hume and Ivey cleverly illustrate reference frames and distinguish between fixed and moving frames of reference.

Frames of Reference (1960) Educational Film

Frames of Reference is a 1960 educational film by Physical Sciences Study Committee. The film was made to be shown in high school physics courses. In the film University of Toronto physics professors Patterson Hume and Donald Ivey explain the distinction between inertial and nonintertial frames of reference, while demonstrating these concepts through humorous camera tricks. For example, the film opens with Dr. Hume, who appears to be upside down, accusing Dr. Ivey of being upside down. Only when the pair flip a coin does it become obvious that Dr. Ivey — and the camera — are indeed inverted. The film's humor serves both to hold students' interest and to demonstrate the concepts being discussed. This PSSC film utilizes a fascinating set consisting of a rotating table and furniture occupying surprisingly unpredictable spots within the viewing area. The fine cinematography by Abraham Morochnik, and funny narration by University of Toronto professors Donald Ivey and Patterson Hume is a wonderful example of the fun a creative team of filmmakers can have with a subject that other, less imaginative types might find pedestrian. Producer: Richard Leacock Production Company: Educational Development Corp. Sponsor: Eric Prestamon

Displacement

Displacement is the change in position of an object relative to its reference frame. For example, if a car moves from a house to a grocery store, its displacement is the relative distance of the grocery store to the reference frame, or the house. The word "displacement" implies that an object has moved or has been displaced. Displacement is the change in position of an object and can be represented mathematically as follows:

$\Delta x = x_f - x_0$

where Δx is displacement, x_f is the final position, and x₀ is the initial position.

shows the importance of using a frame of reference when describing the displacement of a passenger on an airplane.

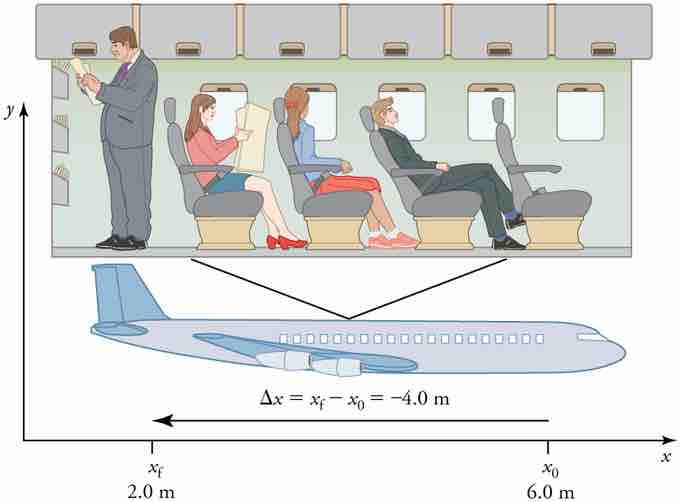
Displacement in Terms of Frame of Reference

A passenger moves from his seat to the back of the plane. His location relative to the airplane is given by x. The -4.0m displacement of the passenger relative to the plane is represented by an arrow toward the rear of the plane. Notice that the arrow representing his displacement is twice as long as the arrow representing the displacement of the professor (he moves twice as far).

[ edit ]

Prev Concept

Defining Kinematics

Introduction to Scalars and Vectors

Next Concept