Induced EMF
The apparatus used by Faraday to demonstrate that magnetic fields can create currents is illustrated in the following figure. When the switch is closed, a magnetic field is produced in the coil on the top part of the iron ring and transmitted (or guided) to the coil on the bottom part of the ring. The galvanometer is used to detect any current induced in a separate coil on the bottom.
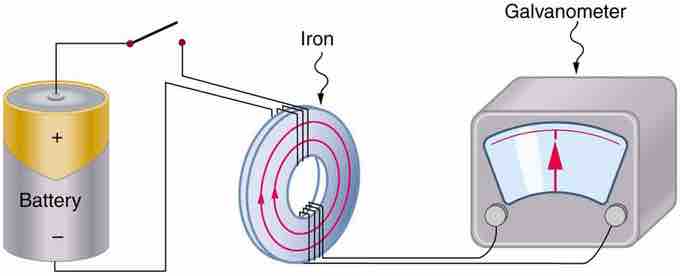
Faraday's Apparatus
This is Faraday's apparatus for demonstrating that a magnetic field can produce a current. A change in the field produced by the top coil induces an EMF and, hence, a current in the bottom coil. When the switch is opened and closed, the galvanometer registers currents in opposite directions. No current flows through the galvanometer when the switch remains closed or open.
It was found that each time the switch is closed, the galvanometer detects a current in one direction in the coil on the bottom. Each time the switch is opened, the galvanometer detects a current in the opposite direction. Interestingly, if the switch remains closed or open for any length of time, there is no current through the galvanometer. Closing and opening the switch induces the current. It is the change in magnetic field that creates the current. More basic than the current that flows is the electromotive force (EMF) that causes it. The current is a result of an EMF induced by a changing magnetic field, whether or not there is a path for current to flow.
Magnetic Flux
The magnetic flux (often denoted Φ or ΦB) through a surface is the component of the magnetic field passing through that surface. The magnetic flux through some surface is proportional to the number of field lines passing through that surface. The magnetic flux passing through a surface of vector area A is
where B is the magnitude of the magnetic field (having the unit of Tesla, T), A is the area of the surface, and θ is the angle between the magnetic field lines and the normal (perpendicular) to A.
For a varying magnetic field, we first consider the magnetic flux
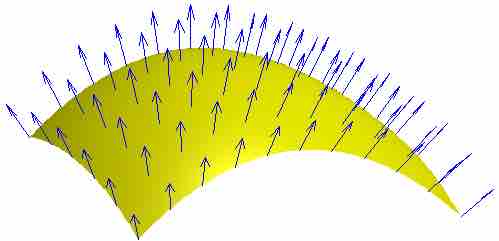
Varying Magnetic Field
Each point on a surface is associated with a direction, called the surface normal; the magnetic flux through a point is then the component of the magnetic field along this normal direction.
A generic surface, A, can then be broken into infinitesimal elements and the total magnetic flux through the surface is then the surface integral