We have studied Faraday's law of induction in previous atoms. We learned the relationship between induced electromotive force (EMF) and magnetic flux. In a nutshell, the law states that changing magnetic field
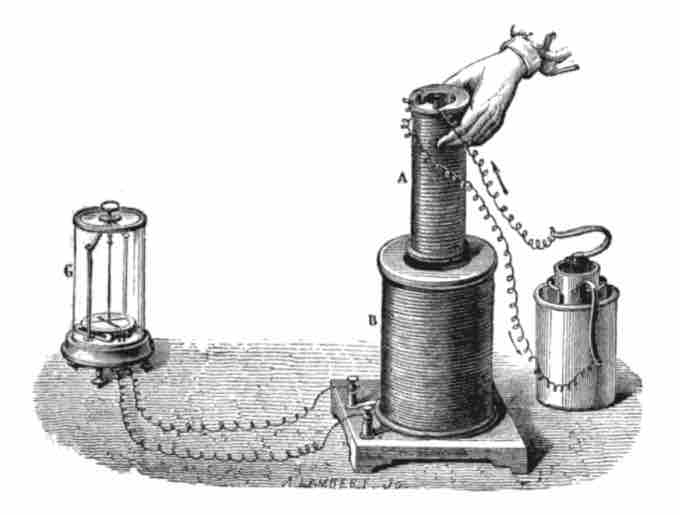
Faraday's Experiment
Faraday's experiment showing induction between coils of wire: The liquid battery (right) provides a current which flows through the small coil (A), creating a magnetic field. When the coils are stationary, no current is induced. But when the small coil is moved in or out of the large coil (B), the magnetic flux through the large coil changes, inducing a current which is detected by the galvanometer (G).
Differential form of Faraday's law
The magnetic flux is
Faraday's law now can be rewritten