When a conductor carries a current, a magnetic field surrounding the conductor is produced. The resulting magnetic flux is proportional to the current. If the current changes, the change in magnetic flux is proportional to the time-rate of change in current by a factor called inductance (L). Since nature abhors rapid change, a voltage (electromotive force, EMF) produced in the conductor opposes the change in current, which is also proportional to the change in magnetic flux. Thus, inductors oppose change in current by producing a voltage that,in turn, creates a current to oppose the change in magnetic flux; the voltage is proportional to the change in current.
Energy Stored in Inductor
Due to energy conservation, the energy needed to drive the original current must have an outlet. For an inductor, that outlet is the magnetic field—the energy stored by an inductor is equal to the work needed to produce a current through the inductor. The formula for this energy is given as:
(Eq. 1), where L is the inductance in units of Henry and I is the current in units of Ampere.
Energy Stored in Magnetic Field
Let's consider Fig 1 , an example of a solenoid (ℓ: length, N: number of turns, I: current, A: cross-section area) that works as an inductor. From Eq. 1, the energy stored in the magnetic field created by the solenoid is:
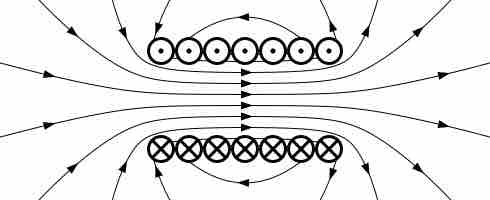
Magnetic Field Created By A Solenoid
Magnetic field created by a solenoid (cross-sectional view) described using field lines. Energy is "stored" in the magnetic field.
(We used the relation
Therefore, the energy density