The Archimedes principle is easiest to understand and apply in the case of entirely submersed objects. In this section we discuss a few relevant examples. In general, the buoyancy force on a completely submerged object is given by the formula:
where
Cylinder
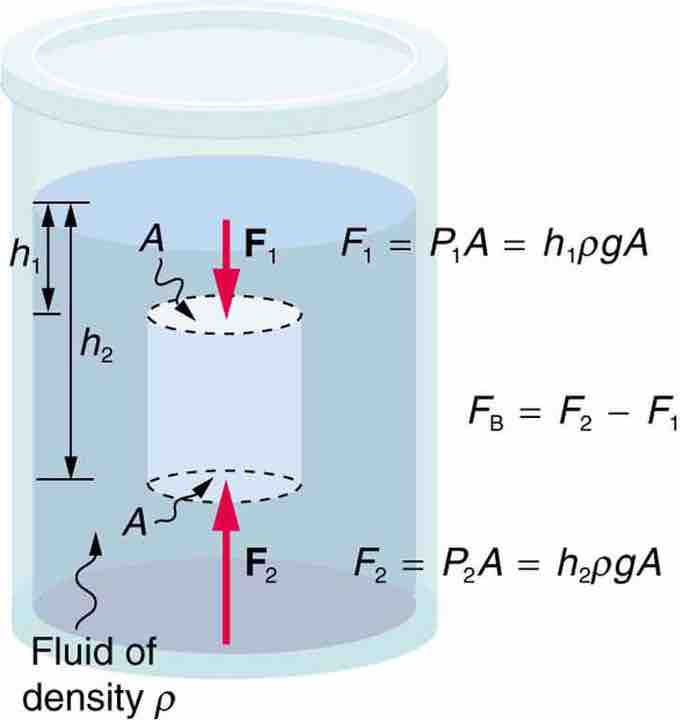
In the previous section, we calculated the buoyancy force on a cylinder (shown in ) by considering the force exerted on each of the cylinder's sides. Now, we'll calculate this force using Archimedes' principle. The buoyancy force on the cylinder is equal to the weight of the displaced fluid. This weight is equal to the mass of the displaced fluid multiplied by the gravitational acceleration:
Buoyant force
The fluid pushes on all sides of a submerged object. However, because pressure increases with depth, the upward push on the bottom surface (F2) is greater than the downward push on the top surface (F1). Therefore, the net buoyant force is always upwards.
The mass of the displaced fluid is equal to its volume multiplied by its density:
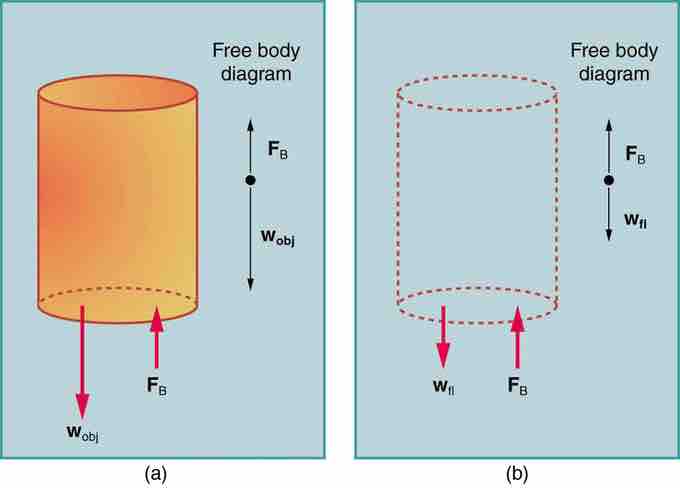
However (and this is the crucial point), the cylinder is entirely submerged, so the volume of the displaced fluid is just the volume of the cylinder (see ), and:
Archimedes principle
The volume of the fluid displaced (b) is the same as the volume of the original cylinder (a).
The volume of a cylinder is the area of its base multiplied by its height, or in our case :
Therefore, the buoyancy force on the cylinder is:
This is the same result obtained in the previous section by considering the force due to the pressure exerted by the fluid.
Helium Airship
Consider the USS Macon, a helium-filled airship (shown in ). Its envelope (the "balloon") contained 184,059.5 cubic meters of helium. Ignoring the small volume of the gondola, what was the buoyancy force on this airship? If the airship weighed 108,000 kg, how much cargo could it carry? Assume the density of air is 1.225 kg per meter cubed. The buoyancy force on an airship is due to the air in which it is immersed. Although we don't know the exact shape of the airship, we know its volume and the density of the air, and thus we can calculate the buoyancy force:

Helium airship
The USS Macon, a 1930s helium-filled airship.
To find the cargo capacity of the airship, we subtract the weight of the airship from the buoyancy force:
The mass the airship can carry is: