A uniform field is that in which the electric field is constant throughout. Just like the so-called "frictionless surface" in mechanics, the uniform field is an ideal but unreal situation that makes for simpler calculations. Equations involving non-uniform electric fields require use of differential calculus.
Uniformity in an electric field can be approximated by placing two conducting plates parallel to one another and creating a potential difference between them. In such a case there will be slight variations in the field near its edges, but it will be approximately constant throughout every other area.
The equation for magnitude of a uniform electric field is:
where E is the field, Δ is the potential difference between the plates, and d is the distance between the plates. The coefficient of -1 arises from the fact that positive charges repel, and thus a positive charge will be pushed away from the positive plate and in a direction opposite that of the increasing voltage.
Uniformity of an electric field allows for simple calculation of work performed when a test charge is moved across it. For the case of a positive charge q to be moved from a point A with a certain potential (V1) to a point B with another potential (V2), that equation is:
The difference (V2-V1) can also be represented as ∆V or VAB. In uniform fields it is also simple to relate ∆V to field strength and distance (d) between points A and B:
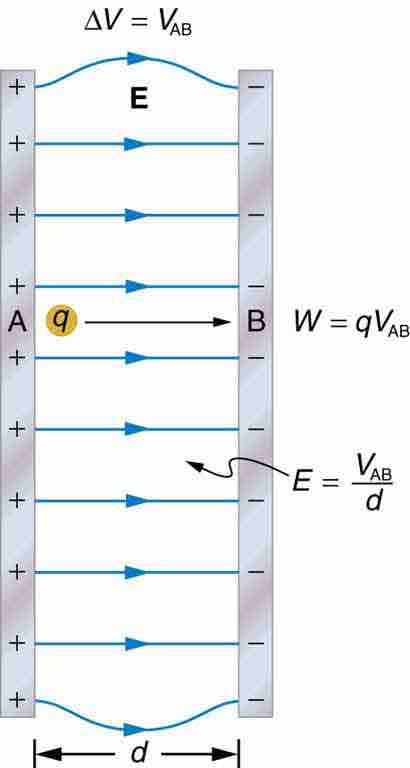
Relationships within a uniform electric field
In this image, Work (W), field strength (E), and potential difference (∆V) are defined for points A and B within the constructs of a uniform potential field between the positive and negative plates.