Relation Between Electric Potential and Field

The relationship between electric potential and field is similar to that between gravitational potential and field in that the potential is a property of the field describing the action of the field upon an object (see ).

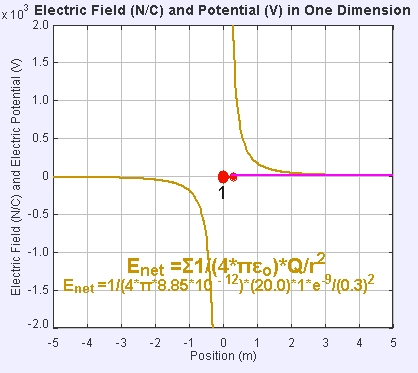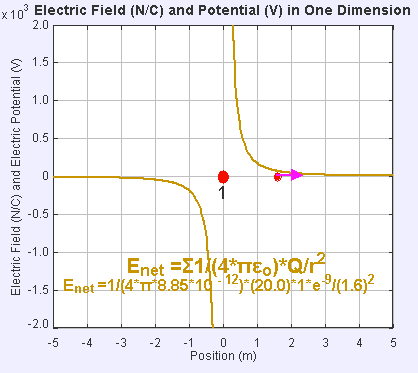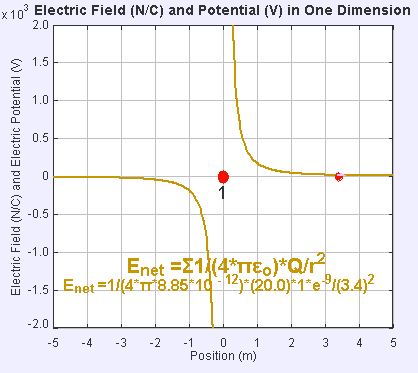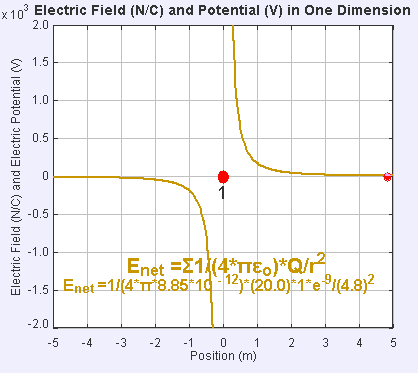
Electric field and potential in one dimension

The presence of an electric field around the static point charge (large red dot) creates a potential difference, causing the test charge (small red dot) to experience a force and move.

The electric field is like any other vector field—it exerts a force based on a stimulus, and has units of force times inverse stimulus. In the case of an electric field the stimulus is charge, and thus the units are NC^-1. In other words, the electric field is a measure of force per unit charge.

The electric potential at a point is the quotient of the potential energy of any charged particle at that location divided by the charge of that particle. Its units are JC^-1. Thus, the electric potential is a measure of energy per unit charge.

In terms of units, electric potential and charge are closely related. They share a common factor of inverse Coulombs (C^-1), while force and energy only differ by a factor of distance (energy is the product of force times distance).

Thus, for a uniform field, the relationship between electric field (E), potential difference between points A and B (Δ), and distance between points A and B (d) is:

$E=- \frac {\Delta \phi}{d}$.

The -1 coefficient arises from repulsion of positive charges: a positive charge will be pushed away from the positively charged plate, and towards a location of higher-voltage.

The above equation is an algebraic relationship for a uniform field. In a more pure sense, without assuming field uniformity, electric field is the gradient of the electric potential in the direction of x:

$E_x=-\frac {dV}{dx}$.

This can be derived from basic principles. Given that ∆P=W (change in the energy of a charge equals work done on that charge), an application of the law of conservation of energy, we can replace ∆P and W with other terms. ∆P can be substituted for its definition as the product of charge (q) and the differential of potential (dV). We can then replace W with its definition as the product of q, electric field (E), and the differential of distance in the x direction (dx):

$qdV=-qE_xdx$.

Dividing both sides of the equation by q yields the previous equation.