Capacitance

Capacitance is the measure of an object's ability to store electric charge.

Learning Objective

Express the relationship between the capacitance, charge of an object, and potential difference in the form of equation

Key Points

The unit of capacitance is known as the farad (F), which can be equated to many quotients of units, including JV^-2, WsV^-2, CV^-1, and C²J^-1.
Capacitance (C) can be calculated as a function of charge an object can store (q) and potential difference (V) between the two plates: $C=\frac {q}{V}$ Q depends on the surface area of the conductor plates, while V depends on the distance between the plates and the permittivity of the dielectric between them.
In storing charge, capacitors also store potential energy, which is equal to the work (W) required to charge them. For a capacitor with plates holding charges of +q and -q, this can be calculated: $W_{stored}=\frac {CV^2}{2}$. The above can be equated with the work required to charge the capacitor.

Terms

dielectric
An electrically insulating or nonconducting material considered for its electric susceptibility (i.e., its property of polarization when exposed to an external electric field).
capacitance
The property of an electric circuit or its element that permits it to store charge, defined as the ratio of stored charge to potential over that element or circuit (Q/V); SI unit: farad (F).

Full Text

Capacitance is the measure of an object's ability to store electric charge. Any body capable of being charged in any way has a value of capacitance.

The unit of capacitance is known as the Farad (F), which can be adjusted into subunits (the millifarad (mF), for example) for ease of working in practical orders of magnitude. The Farad can be equated to many quotients of units, including JV^-2, WsV^-2, CV^-1, and C²J^-1.

The most common capacitor is known as a parallel-plate capacitor which involves two separate conductor plates separated from one another by a dielectric . Capacitance (C) can be calculated as a function of charge an object can store (q) and potential difference (V) between the two plates:

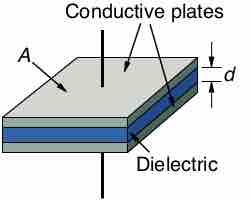
Parallel-Plate Capacitor

The dielectric prevents charge flow from one plate to the other.

$C=\frac {q}{V}$

Ultimately, in such a capacitor, q depends on the surface area (A) of the conductor plates, while V depends on the distance (d) between the plates and the permittivity (ε_r) of the dielectric between them. For a parallel-plate capacitor, this equation can be used to calculate capacitance:

$C=\epsilon_r \epsilon_0 \frac {A}{d}$

Where ε₀ is the electric constant. The product of length and height of the plates can be substituted in place of A.

In storing charge, capacitors also store potential energy, which is equal to the work (W) required to charge them. For a capacitor with plates holding charges of +q and -q, this can be calculated:

$W_{charging}=\int_0^Q \! \frac {q}{C} \mathrm{d} q=\frac {CV^2}{2}=W_{stored}$

Thus, either through calculus or algebraically (if C and V are known), stored energy (W_stored) can be calculated. In a parallel-plate capacitor, this can be simplified to:

$W_{stored}= \frac {\epsilon_r \epsilon_0 AV^2}{2d}$

[ edit ]

Prev Concept

Superposition of Electric Potential

Capacitors with Dielectrics

Next Concept