Combination Circuits
More complex connections of resistors are sometimes just combinations of series and parallel. This is commonly encountered, especially when wire resistances is considered. In that case, wire resistance is in series with other resistances that are in parallel.
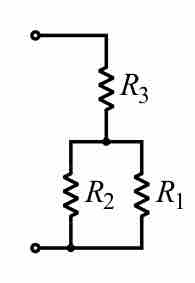
A combination circuit can be broken up into similar parts that are either series or parallel, as diagrammed in . In the figure, the total resistance can be calculated by relating the three resistors to each other as in series or in parallel. R1 and R2 are connected in parallel in relation to each other, so we know that for that subset, the inverse of resistance would be equal to:
Resistor Network
In this combination circuit, the circuit can be broken up into a series component and a parallel component.
R3 is connected in series to both R1 and R2, so the resistance would be calculated as:
Complex Combination Circuits
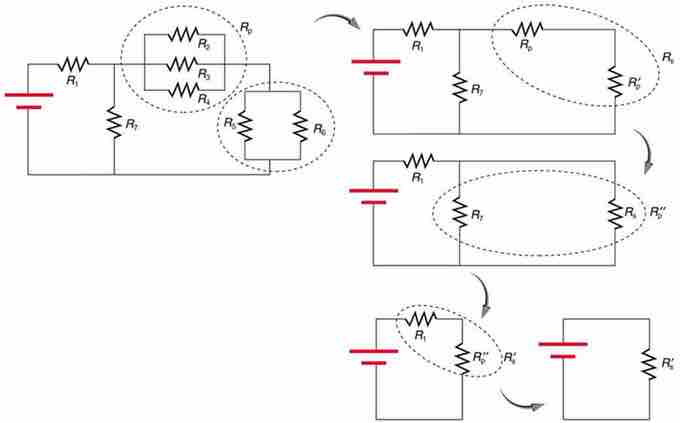
For more complicated combination circuits, various parts can be identified as series or parallel, reduced to their equivalents, and then further reduced until a single resistance is left, as shown in . In this figure, the combination of seven resistors was identified by being either in series or in parallel. In the initial image, the two circled sections show resistors that are in parallel.
Reducing a combination circuit
This combination of seven resistors has both series and parallel parts. Each is identified and reduced to an equivalent resistance, and these are further reduced until a single equivalent resistance is reached.
Reducing those parallel resistors into a single R value allows us to visualize the circuit in a more simplified manner. In the top right image, we can see that the circled portion contains two resistors in series. We can further reduce that to another R value by adding them. The next step shows that the circled two resistors are in parallel. Reducing those highlights that the last two are in series, and thus can be reduced to a single resistance value for the entire circuit.
One practical implication of a combination circuit is that resistance in wires reduces the current and power delivered to a resistor. Combination circuit can be transformed into a series circuit, based on an understanding of the equivalent resistance of parallel branches to a combination circuit. A series circuit can be used to determine the total resistance of the circuit. Essentially, wire resistance is a series with the resistor. It thus increases the total resistance and decreases the current. If wire resistance is relatively large, as in a worn (or a very long) extension cord, then this loss can be significant. If a large current is drawn, the IR drop in the wires can also be significant.