Kirchhoff's loop rule (otherwise known as Kirchhoff's voltage law (KVL), Kirchhoff's mesh rule, Kirchhoff's second law, or Kirchhoff's second rule) is a rule pertaining to circuits, and is based on the principle of conservation of energy.
Conservation of energy—the principle that energy is neither created nor destroyed—is a ubiquitous principle across many studies in physics, including circuits. Applied to circuitry, it is implicit that the directed sum of the electrical potential differences (voltages) around any closed network is equal to zero. In other words, the sum of the electromotive force (emf) values in any closed loop is equal to the sum of the potential drops in that loop (which may come from resistors).
Another equivalent statement is that the algebraic sum of the products of resistances of conductors (and currents in them) in a closed loop is equal to the total electromotive force available in that loop. Mathematically, Kirchhoff's loop rule can be represented as the sum of voltages in a circuit, which is equated with zero:
Here, Vk is the voltage across element k, and n is the total number of elements in the closed loop circuit. An illustration of such a circuit is shown in . In this example, the sum of v1, v2, v3, and v4 (and v5 if it is included), is zero.
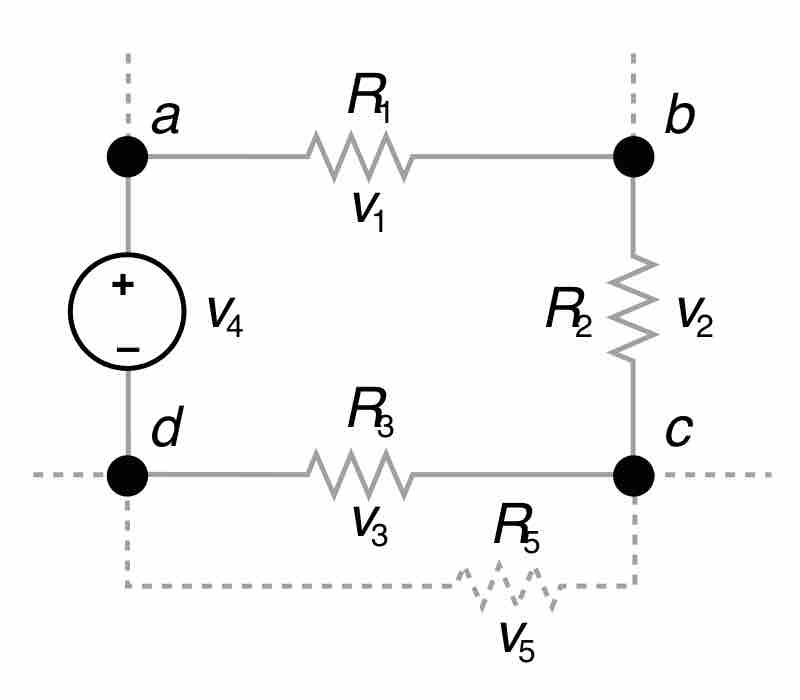
Kirchhoff's Loop Rule
Kirchhoff's loop rule states that the sum of all the voltages around the loop is equal to zero: v1 + v2 + v3 - v4 = 0.
Given that voltage is a measurement of energy per unit charge, Kirchhoff's loop rule is based on the law of conservation of energy, which states: the total energy gained per unit charge must equal the amount of energy lost per unit of charge.
Example
illustrates the changes in potential in a simple series circuit loop. Kirchhoff's second rule requires emf−Ir−IR1−IR2=0. Rearranged, this is emf=Ir+IR1+IR2, meaning that the emf equals the sum of the IR (voltage) drops in the loop. The emf supplies 18 V, which is reduced to zero by the resistances, with 1 V across the internal resistance, and 12 V and 5 V across the two load resistances, for a total of 18 V.
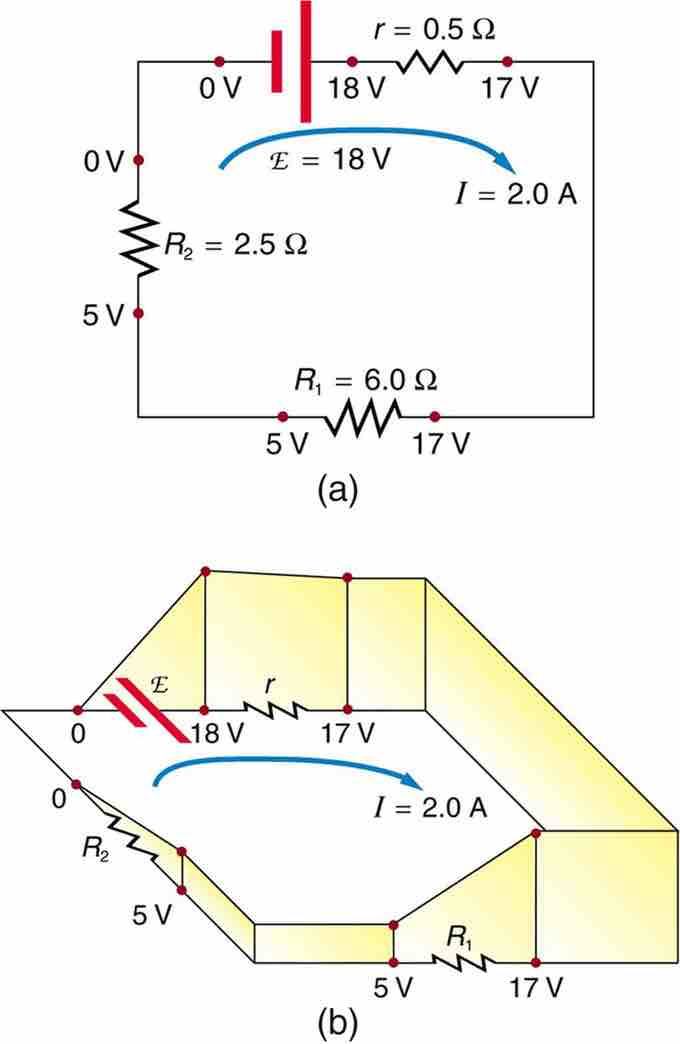
The Loop Rule
An example of Kirchhoff's second rule where the sum of the changes in potential around a closed loop must be zero. (a) In this standard schematic of a simple series circuit, the emf supplies 18 V, which is reduced to zero by the resistances, with 1 V across the internal resistance, and 12 V and 5 V across the two load resistances, for a total of 18 V. (b) This perspective view represents the potential as something like a roller coaster, where charge is raised in potential by the emf and lowered by the resistances. (Note that the script E stands for emf. )
Limitation
Kirchhoff's loop rule is a simplification of Faraday's law of induction, and holds under the assumption that there is no fluctuating magnetic field linking the closed loop. In the presence of a variable magnetic field, electric fields could be induced and emf could be produced, in which case Kirchhoff's loop rule breaks down.