In an oligopoly, firms are interdependent; they are affected not only by their own decisions regarding how much to produce, but by the decisions of other firms in the market as well. Game theory offers a useful framework for thinking about how firms may act in the context of this interdependence. More specifically, game theory can be used to model situations in which each actor, when deciding on a course of action, must also consider how others might respond to that action.
For example, game theory can explain why oligopolies have trouble maintaining collusive arrangements to generate monopoly profits. While firms would be better off collectively if they cooperate, each individual firm has a strong incentive to cheat and undercut their competitors in order to increase market share. Because the incentive to defect is strong, firms may not even enter into a collusive agreement if they don't perceive there to be a way to effectively punish defectors.
The prisoner's dilemma is a specific type of game in game theory that illustrates why cooperation may be difficult to maintain for oligopolists even when it is mutually beneficial. In the game, two members of a criminal gang are arrested and imprisoned. The prisoners are separated and left to contemplate their options . If both prisoners confess, each will serve a two-year prison term. If one confesses, but the other denies the crime, the one that confessed will walk free, while the one that denied the crime would get a three-year sentence. If both deny the crime, they will both serve only a one year sentence. Betraying the partner by confessing is the dominant strategy; it is the better strategy for each player regardless of how the other plays. This is known as a Nash equilibrium. The result of the game is that both prisoners pursue individual logic and betray, when they would have collectively gotten a better outcome if they had both cooperated.
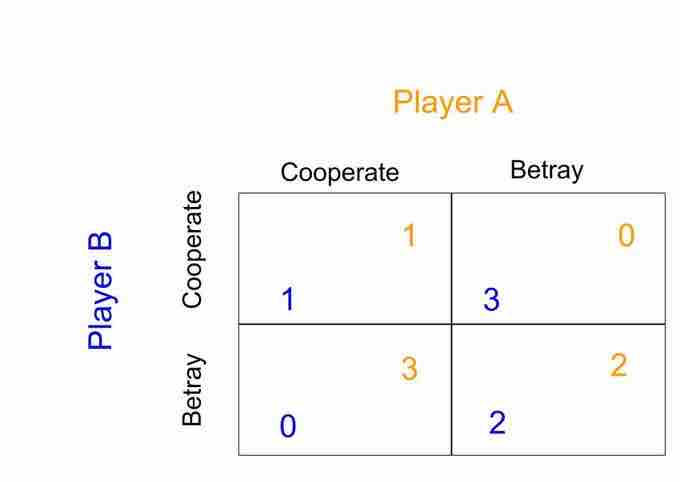
Prisoner's Dilemma
In a prisoner's dilemma game, the dominant strategy for each player is to betray the other, even though cooperation would have led to a better collective outcome.
The Nash equilibrium is an important concept in game theory. It is the set of strategies such that no player can do better by unilaterally changing his or her strategy. If a player knew the strategies of the other players (and those strategies could not change), and could not benefit by changing his or her strategy, then that set of strategies represents a Nash equilibrium. If any player would benefit by changing his or her strategy, then that set of strategies is not a Nash equilibrium.
While game theory is important to understanding firm behavior in oligopolies, it is generally not needed to understand competitive or monopolized markets. In competitive markets, firms have such a small individual effect on the market, that taking other firms into account is simply not necessary. A monopolized market has only one firm, and thus strategic interactions do not occur.