Derivation of Hess's Law
Hess's law is a relationship in physical chemistry named after Germain Hess, a Swiss-born Russian chemist and physician. This law states that if a reaction takes place in several steps, then the standard reaction enthalpy for the overall reaction is equal to the sum of the standard enthalpies of the intermediate reaction steps, assuming each step takes place at the same temperature.
Hess's law derives directly from the law of conservation of energy, as well as its expression in the first law of thermodynamics. Since enthalpy is a state function, the change in enthalpy between products and reactants in a chemical system is independent of the pathway taken from the initial to the final state of the system. Hess's law can be used to determine the overall energy required for a chemical reaction, especially when the reaction can be divided into several intermediate steps that are individually easier to characterize. Negative enthalpy change for a reaction indicates exothermic process, while positive enthalpy change corresponds to endothermic process.
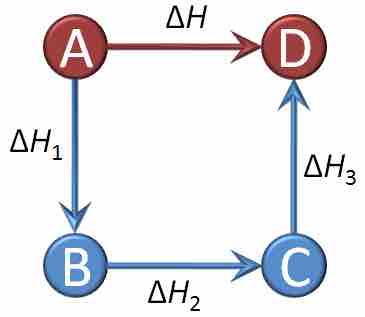
Graphical representation of Hess's law
The net reaction here is A being converted into D, and the change in enthalpy for that reaction is ΔH. However, we can see that the net reaction is a result of A being converted into B, which is then converted into C, which is finally converted into D. By Hess's law, the net change in enthalpy of the overall reaction is equal to the sum of the changes in enthalpy for each intermediate transformation: ΔH = ΔH1+ΔH2+ΔH3.
Calculating Standard Enthalpies of Reaction Using Hess's Law
Turning graphite into diamond requires extremely high temperatures and pressures, and therefore is impractical in a laboratory setting. The change in enthalpy for this reaction cannot be determined experimentally. However, because we know the standard enthalpy change for the oxidation for these two substances, it is possible to calculate the enthalpy change for this reaction using Hess's law. Our intermediate steps are as follows:
In order to get these intermediate reactions to add to our net overall reaction, we need to reverse the second step. Keep in mind that when reversing reactions using Hess's law, the sign of ΔH will change. Sometimes, you will need to multiply a given reaction intermediate through by an integer. In such cases, you need always multiply your ΔH value by that same integer. Restating the first equation and flipping the second equation, we have:
Adding these equations together, carbon dioxides and oxygens cancel, leaving us only with our net equation. By Hess's law, we can sum the ΔH values for these intermediate reactions to get our final value,