Capillary Action

Cohesion and Adhesion

The molecules in any sample of matter experience intermolecular forces, which are attractive or repulsive forces between atoms or molecules within the sample. Such forces are responsible for many observable behaviors of substances, such as the phase they are in under certain conditions of temperature and pressure. When attractive forces occur between like molecules, they are referred to as cohesive forces, or resulting in cohesion, because they hold the molecules of sample close together. These cohesive forces are especially strong at the surface of a liquid, resulting in the phenomenon of surface tension. For example, the hydrogen bonds between water molecules are responsible for the cohesion observed in water droplets.

On the other hand, when intermolecular forces occur between different types of molecules (especially when they are part of different phases of matter), they are referred to as adhesive forces, or resulting in adhesion. The molecules in a sample of water in contact with a glass surface experience attractive forces toward the glass molecules. Water has a tendency to adhere to such surfaces because of those interactions.

Capillary Action

Capillary action is the ability of a liquid to flow in narrow spaces without the assistance of, and in opposition to, external forces such as gravity. This effect can be seen in the drawing-up of liquids between the hairs of a paintbrush, in a thin tube, in porous materials such as paper, in some non-porous materials (such as liquified carbon fiber), or in a cell. It occurs when the intermolecular attractive forces between the liquid and the solid surrounding surfaces (adhesive forces) are stronger than the cohesive forces within the liquid. If the diameter of the tube is sufficiently small, then the combination of surface tension (which is caused by cohesion within the liquid) and adhesive forces between the liquid and container act together to lift the liquid. The height (h) of a liquid column is given by:

$h = \frac {2T} {\rho r g}$

where T is the surface tension, $\rho$ is the density of liquid, g is the acceleration due to gravity, and r is radius of the tube. Notice that the height to which the liquid is lifted is inversely proportional to the radius of the tube, which explains why the phenomenon is more pronounced for smaller tubes.

Consider a water-filled glass tube with a radius of 2 cm (0.02 m) in air at standard laboratory conditions, T = 0.0728 N/m at 20 °C, $\rho$ is 1000 kg/m³, and g = 9.81 m/s². For these values, the height of the water column is 0.74 mm. By comparison, for a 4 m diameter glass tube in the lab conditions given above (radius 2 m, or 6.6 ft), the water would rise an unnoticeable 0.007 mm (0.00028 in). For a 0.4-mm (0.016-in) diameter tube (radius 0.2 mm, or 0.0079 in), the water would rise 70 mm (2.8 in).

A common apparatus used to demonstrate capillary action is the capillary tube. When the lower end of a vertical glass tube is placed in a liquid, a concave meniscus forms. Adhesion forces between the fluid and the solid inner wall pull the liquid column up until there is a sufficient mass of liquid for gravitational forces to counteract these forces.

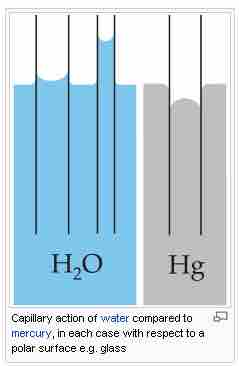
Capillary action in glass tubes

The rise or fall of liquids in a capillary tube depends upon the interactions between the tube and the liquid.

The meniscus is the curve caused by surface tension in the upper surface of a liquid. It can be either convex or concave. A convex meniscus occurs when the molecules have a stronger attraction to each other (cohesion) than to the material of the container (adhesion), causing the surface of the liquid to cave downward. This may be seen between mercury and glass in barometers and thermometers. Conversely, a concave meniscus occurs when the molecules of the liquid are attracted to those of the container, causing the surface of the liquid to cave upwards. This can be seen in a glass of water.

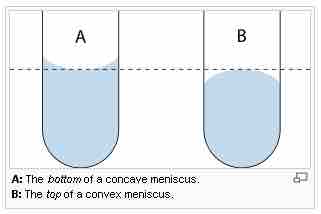
The meniscus curve on a column of fluid in a capillary tube

The curvature of the surface at the top of a column of fluid in a narrow tube is caused by the relative strength of the forces responsible for the surface tension of the fluid (cohesive forces) and the adhesive forces to the walls of the container.

Capillary action acts on concave menisci to pull the liquid up, increasing the favorable contact area between liquid and container, and on convex menisci to pull the liquid down, reducing the amount of contact area.

When considering how liquids will behave on surfaces, if the liquid molecules are strongly attracted to the solid molecules then the liquid drop will completely spread out on the solid surface. This is often the case for water on bare metallic or ceramic surfaces.

The phenomenon of capillary action is important in the transport of water and nutrients in plants through the process of transpiration.