The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted by an atom's electrons when they are returned to a lower energy state. Each element's emission spectrum is unique, and therefore spectroscopy can be used to identify elements present in matter of unknown composition. Similarly, the emission spectra of molecules can be used in chemical analysis of substances.
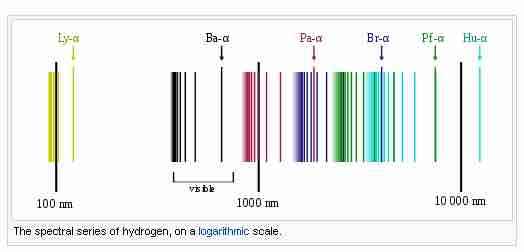
Emission spectrum of atomic hydrogen
Spectral series of hydrogen.
The emission spectrum of atomic hydrogen is divided into a number of spectral series, with wavelengths given by the Rydberg formula:
where R is the Rydberg constant (approximately 1.09737 x 107 m-1),
The spectral lines are grouped into series according to n′. Lines are named sequentially starting from the longest wavelength/lowest frequency of the series using Greek letters within each series. For example, the 2 → 1 line is called Lyman-alpha (Ly-α), while the 7 → 3 line is called Paschen-delta (Pa-δ). Some hydrogen spectral lines fall outside these series, such as the 21 cm line (these correspond to much rarer atomic events such as hyperfine transitions). The fine structure also results in single spectral lines appearing as two or more closely grouped thinner lines due to relativistic corrections. Typically, one can only observe these series from pure hydrogen samples in a lab. Many of the lines are very faint and additional lines can be caused by other elements (such as helium if using sunlight or nitrogen in the air). Lines outside of the visible spectrum typically cannot be seen in observations of sunlight, as the atmosphere absorbs most infrared and ultraviolet wavelengths through the action of water vapor and ozone molecules respectively.
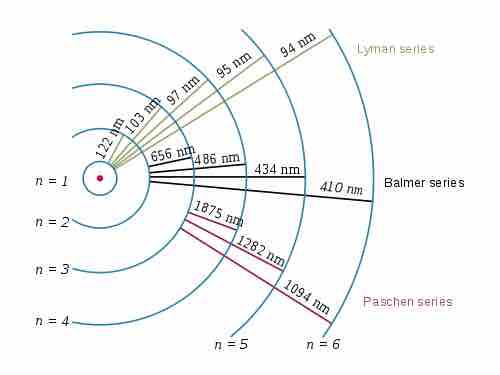
Electron transitions and their resulting wavelengths for hydrogen
Three of the transition series in hydrogen (not to scale).
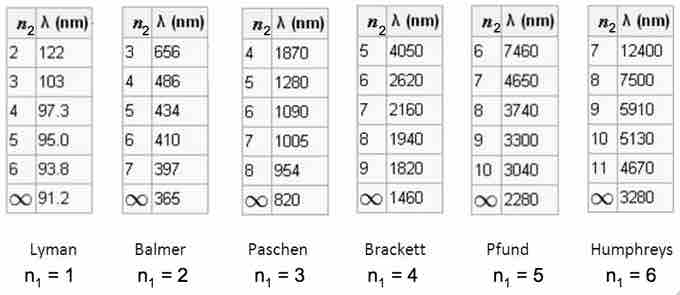
The emission spectrum of hydrogen
Some of the most common and readily observable series have been named as shown in this image, where n1 is the ground state and n2 are excited states. The various series are named for the atomic energy level they end on (n1). The series limit where n2 is infinite and n1=1 corresponds to the ionization energy of hydrogen.