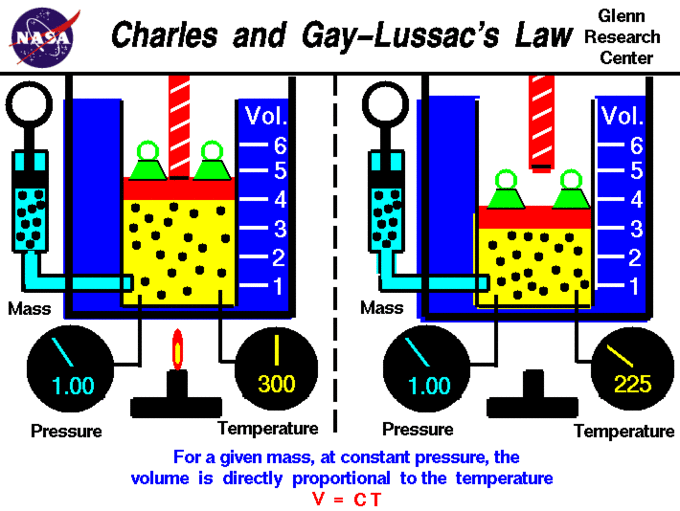
Charles' and Guy-Lussac's Law
Charles' Law describes the relationship between the volume and temperature of a gas. The law was first published by Joseph Louis Gay-Lussac in 1802, but he referenced unpublished work by Jacques Charles from around 1787. This law states that at constant pressure, the volume of a given mass of an ideal gas increases or decreases by the same factor as its temperature (in Kelvin); in other words, temperature and volume are directly proportional. Stated mathematically, this relationship is:
Example
- A car tire filled with air has a volume of 100 L at 10°C. What will the expanded volume of the tire be after driving the car has raised the temperature of the tire to 40°C?
-
$\frac {V_1}{T_1}=\frac{V_2}{T_2}$ -
$\frac {\text{100 L}}{\text{283 K}}=\frac{V_2}{\text{313 K}}$ -
$V_2=\text{110 L}$
V vs. T Plot and Charles' Law
A visual expression of Charles' and Gay-Lussac's Law is shown in a graph of the volume of one mole of an ideal gas as a function of its temperature at various constant pressures. The plots show that the ratio
Charles' and Gay–Lussac's Law
A visual expression of the law of Charles and Gay-Lussac; specifically, a chart of the volume of one mole of an ideal gas as a function of its temperature at various constant pressures.
Extrapolation to Zero Volume
If a gas contracts by 1/273 of its volume for each degree of cooling, it should contract to zero volume at a temperature of –273°C; this is the lowest possible temperature in the universe, known as absolute zero. This extrapolation of Charles' Law was the first evidence of the significance of this temperature.
Why Do the Plots for Different Pressures Have Different Slopes?
The lower a gas' pressure, the greater its volume (Boyle's Law), so at low pressures, the fraction \frac{V}{273} will have a larger value; therefore, the gas must "contract faster" to reach zero volume when its starting volume is larger.