pH and pOH
Recall the reaction for the autoionization of water:
This reaction has a special equilibrium constant denoted KW, and it can be written as follows:
Because H+ and OH- dissociate in a one-to-one molar ratio,
If we take the negative logarithm of each concentration, we get:
Here we have the reason that neutral water has a pH of 7.0 -; this is the pH at which the concentrations of H+ and OH- are exactly equal.
Lastly, we should take note of the following relationship:
This relationship will always apply to aqueous solutions. It is a quick and convenient way to find pH from pOH, hydrogen ion concentration from hydroxide ion concentration, and more.
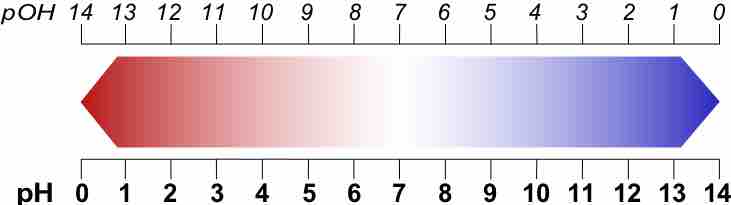
The pH and pOH Scale
Relation between p[OH] and p[H] (brighter red is more acidic, which is the lower numbers for the pH scale and higher numbers for the pOH scale; brighter blue is more basic, which is the higher numbers for the pH scale and lower numbers for the pOH scale).
pKa and pKb
Generically, this p-notation can be used for other scales. In acid-base chemistry, the amount by which an acid or base dissociates to form H+ or OH- ions in solution is often given in terms of their dissociation constants (Ka or Kb). However, because these values are often very small for weak acids and weak bases, the p-scale is used to simplify these numbers and make them more convenient to work with. Quite often we will see the notation pKa or pKb, which refers to the negative logarithms of Ka or Kb, respectively.