Integration By Parts
Integration By Parts
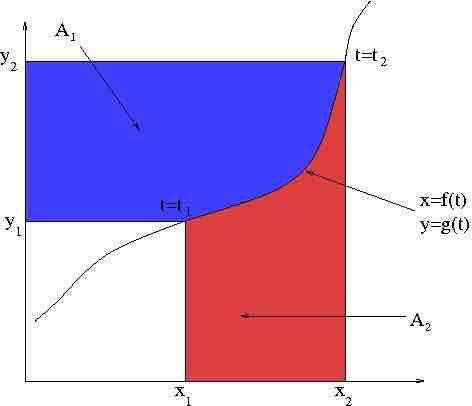
Integration by parts may be thought of as deriving the area of the blue region from the total area and that of the red region. The area of the blue region is
Source
Boundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources: