An alternating series is an infinite series of the form:
or:
with
Alternating Series Test
The theorem known as the "Leibniz Test," or the alternating series test, tells us that an alternating series will converge if the terms
Proof: Suppose the sequence
Since
Example:
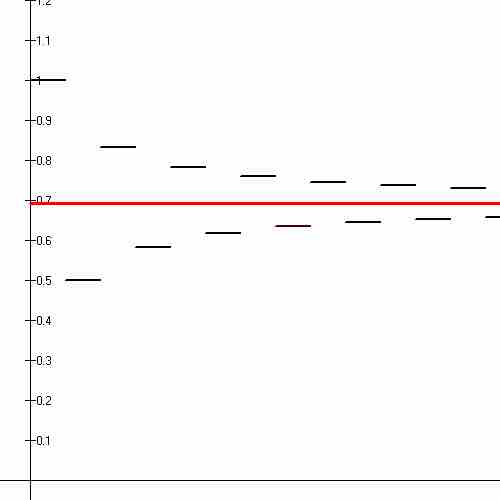
Alternating Harmonic Series
The first fourteen partial sums of the alternating harmonic series (black line segments) shown converging to the natural logarithm of 2 (red line).