An infinite series of numbers is said to converge absolutely (or to be absolutely convergent) if the sum of the absolute value of the summand is finite. More precisely, a real or complex series
Absolute convergence is important for the study of infinite series because its definition is strong enough to have properties of finite sums that not all convergent series possess, yet is broad enough to occur commonly. (A convergent series that is not absolutely convergent is called conditionally convergent.)
Ratio Test
The ratio test is a test (or "criterion") for the convergence of a series
The usual form of the test makes use of the limit,
- if
$L < 1$ , then the series converges absolutely; - if
$L > 1$ , then the series does not converge; - if
$L = 1$ or the limit fails to exist, then the test is inconclusive, because there exist both convergent and divergent series that satisfy this case.
Root Test
The root test is a criterion for the convergence (a convergence test) of an infinite series. It depends on the quantity
The root test was developed first by Augustin-Louis Cauchy and so is sometimes known as the Cauchy root test, or Cauchy's radical test. For a series
- if
$C < 1$ , then the series converges absolutely; - if
$C > 1$ , then the series diverges; - if
$C = 1$ and the limit approaches strictly from above, then the series diverges; - otherwise the test is inconclusive (the series may diverge, converge absolutely, or converge conditionally).
There are some series for which
and there are others for which
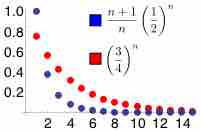
Ratio Test
In this example, the ratio of adjacent terms in the blue sequence converges to