The Derivative as a Function

Let $f$ be a function that has a derivative at every point $a$ in the domain of $f$. Because every point $a$ has a derivative, there is a function that sends the point $a$ to the derivative of $f$ at $a$. This function is written $f'(x)$ and is called the derivative function or the derivative of $f$. The derivative of $f$ collects all the derivatives of $f$ at all the points in the domain of $f$. Visually, derivative of a function $f$ at $x=a$ represents the slope of the curve at the point $x=a$.

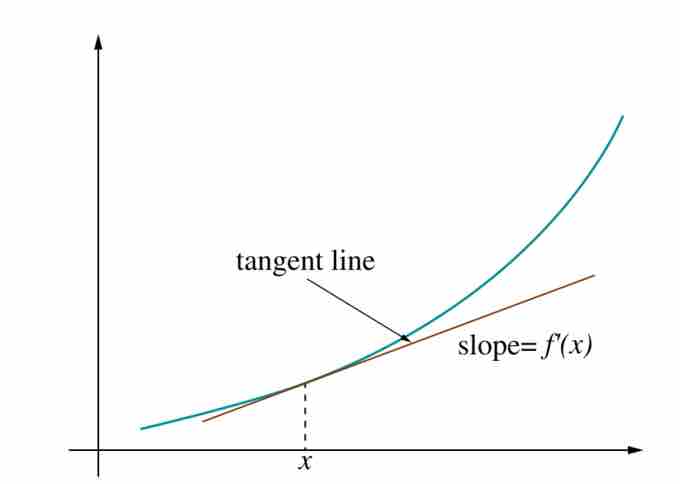
Derivative As Slope

The slope of tangent line shown represents the value of the derivative of the curved function at the point $x$.

Sometimes $f$ has a derivative at most, but not all, points of its domain. The function whose value at $a$ equals $f'(a)$ whenever $f'(a)$ is defined and elsewhere is undefined is also called the derivative of $f$. It is still a function, but its domain is strictly smaller than the domain of $f$.

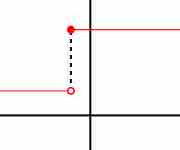
Discontinuous Function

At the point where the function makes a jump, the derivative of the function does not exist.

Using this idea, differentiation becomes a function of functions: The derivative is an operator whose domain is the set of all functions that have derivatives at every point of their domain and whose range is a set of functions. If we denote this operator by $D$, then $D(f)$ is the function $f'(x)$. Since $D(f)$ is a function, it can be evaluated at a point $a$. By the definition of the derivative function, $D(f)(a)=f'(a)$.

For comparison, consider the doubling function $f(x) = 2x$; $f$ is a real-valued function of a real number, meaning that it takes numbers as inputs and has numbers as outputs:

$1 \rightarrow 2$

$2 \rightarrow 4$

$3 \rightarrow 6$.

The operator $D$, however, is not defined on individual numbers. It is only defined on functions:

$D(x \rightarrow 1) = (x \rightarrow 0)$

$D(x \rightarrow x) = (x \rightarrow 1)$

$D(x \rightarrow x^2) = (x \rightarrow 2x)$.

Because the output of $D$ is a function, the output of $D$ can be evaluated at a point. For instance, when $D$ is applied to the squaring function,

$x \rightarrow x^2$

$D$ outputs the doubling function,

$x \rightarrow 2x$

which is f(x)f(x). This output function can then be evaluated to get f(1)=2f(1) = 2, $f(2) = 4$, and so on.