Average Value of a Function

An average is a measure of the "middle" or "typical" value of a data set. It is a measure of central tendency. In the most common case, the data set is a discrete set of numbers. The average of a list of numbers is a single number intended to typify the numbers in the list, which is called the arithmetic mean. However, the concept of average can be extended to functions as well.

If $n$ numbers are given, each number denoted by $a_i$, where $i = 1, \cdots , n$, the arithmetic mean is the sum of all $a_i$ values divided by $n$:

 $\displaystyle{AM=\frac{1}{n}\sum_{i=1}^na_i}$

extend this definition to continuum by making the following substitution: 

$\displaystyle{\sum \rightarrow \int, a_i \rightarrow f(x), \frac{1}{n} \rightarrow \frac{dx}{b-a}}$

Therefore, the average of a function $f(x)$ over an interval $[a,b]$ (where $b > a$) is expressed as:

 $\displaystyle{\bar f = \frac{1}{b-a} \int_a^b f(x) \ dx}$

Note that the average is equal to the area under the curve, $S$, divided by the range:

 $\displaystyle{\frac{S}{b-a}}$

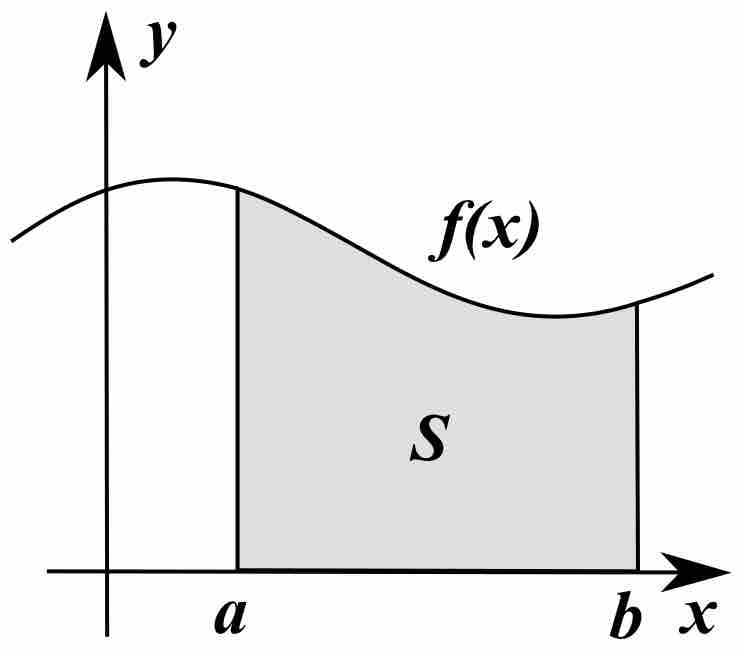
Fig 1

The average of a function $f(x)$ that has area $S$ over the range $[a,b]$ is $\frac{S}{b-a}$.

Mean Value Theorem for Integration

The first mean value theorem for integration states that if $G : [a, b] \to R$ is a continuous function and $\varphi$ is an integrable function that does not change sign on the interval $(a, b)$, then there exists a number $x$ in $(a, b)$ such that:

 $\displaystyle{\int_a^b G(t)\varphi (t) \, dt=G(x) \int_a^b \varphi (t) \, dt}$

In particular, if $\varphi(t) = 1$ for all $t$ in $[a, b] $, then there exists $x$ in $(a, b)$ such that:

 $\displaystyle{\int_a^b G(t) \, dt=\ G(x)(b - a)}$

The value $G(x)$ is the mean value of $G(t)$ on $[a, b] $ as we saw previously.