In calculus, the mean value theorem states, roughly: given a planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints .
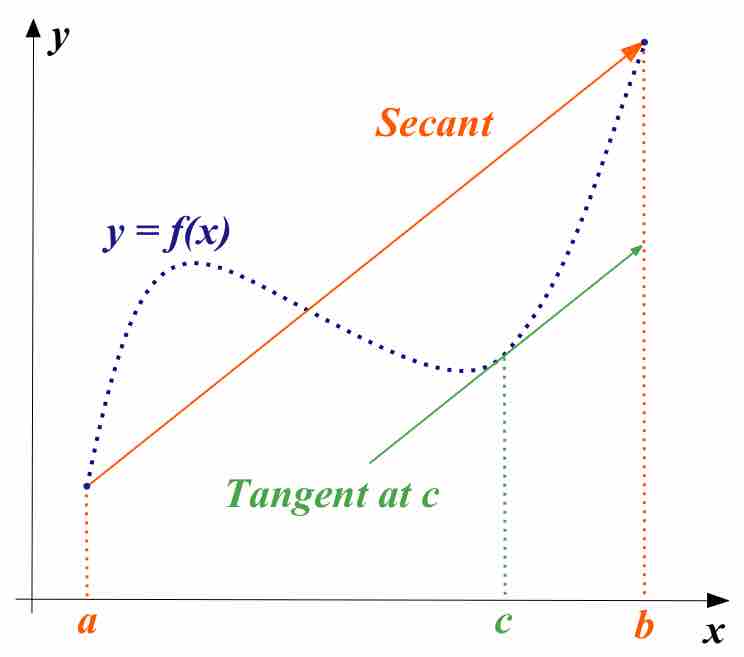
Mean Value Theorem
For any function that is continuous on
The theorem is used to prove global statements about a function on an interval starting from local hypotheses about derivatives at points of the interval. More precisely, if a function
This theorem can be understood intuitively by applying it to motion: If a car travels one hundred miles in one hour, then its average speed during that time was 100 miles per hour. To get at that average speed, the car either has to go at a constant 100 miles per hour during that whole time, or, if it goes slower at one moment, it has to go faster at another moment as well (and vice versa), in order to still end up with an average of 100 miles per hour. Therefore, the Mean Value Theorem tells us that at some point during the journey, the car must have been traveling at exactly 100 miles per hour; that is, it was traveling at its average speed.
The mean value theorem follows from the more specific statement of Rolle's theorem, and can be used to prove the more general statement of Taylor's theorem (with Lagrange form of the remainder term).
Rolle's Theorem states that if a real-valued function