Differentials

In calculus, the differential represents the principal part of the change in a function $y = f(x)$ with respect to changes in the independent variable. The differential $dy$ is defined by:

$dy=f'(x)dx$

where $f'(x)$ is the derivative of $f$ with respect to $x$, and $dx$ is an additional real variable (so that $dy$ is a function of $x$ and $dx$). The notation is such that the equation

$\displaystyle{dy=\frac{dy}{dx}dx}$

holds, where the derivative is represented in the Leibniz notation $\frac{dy}{dx}$, and this is consistent regarding the derivative as the quotient of the differentials. One also writes:

$df (x) = f'(x) dx$

The precise meaning of the variables $dy$ and $dx$ depends on the context of the application and the required level of mathematical rigor. The domain of these variables may take on a particular geometrical significance if the differential is regarded as a particular differential form, or a particular analytical significance if the differential is regarded as a linear approximation to the increment of a function. In physical applications, the variables $dx$ and $dy$ are often constrained to be very small ("infinitesimal").

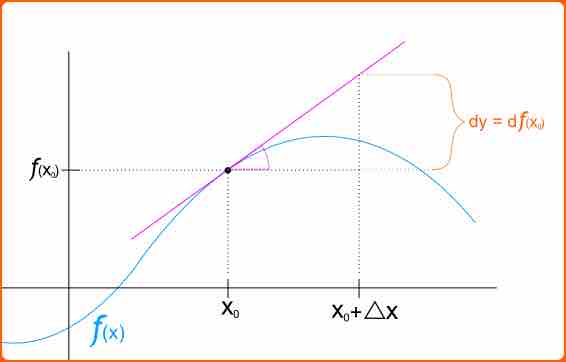
Differentials

The differential of a function $f(x)$ at a point $x_0$.

Higher-order differentials of a function $y = f(x)$ of a single variable $x$ can be defined as follows:

$d(dy)=d(f'(x))$

and, in general:

$\displaystyle{d^n(y)=f^{(n)}(x)(dx)^n}$

Informally, this justifies Leibniz's notation for higher-order derivatives.

When the independent variable $x$ itself is permitted to depend on other variables, then the expression becomes more complicated, as it must also include higher-order differentials in $x$ itself. Thus, for instance,

$d^2(y)=f''(x)(dx)^2+f'(x)(d^2x)$

and so forth.