Precise Definition of a Limit

The $(\varepsilon,\delta)$-definition of limit ("epsilon-delta definition of limit") is a formalization of the notion of limit. It was first given by Bernard Bolzano in 1817, followed by a less precise form by Augustin-Louis Cauchy. The definitive modern statement was ultimately provided by Karl Weierstrass.

The $(\varepsilon,\delta)$-Definition

The $(\varepsilon,\delta)$-definition of limit is a formalization of the notion of limit. Suppose $f:R \rightarrow R$ is defined on the real line and $p,L \in R$. It is said the limit of $f$ as $x$ approaches $p$ is $L$ and written $lim_{x} \rightarrow pf(x)=L\lim_{x \to p}f(x) = L$, if the following property holds:

• For every real $\varepsilon > 0$, there exists a real $\delta > 0$ such that for all real $x$, $\varepsilon > 0$ $0 < \left | x-p \right | < \delta$ implies $\left | f(x) - L \right | < \varepsilon$. Note that the value of the limit does not depend on the value of $f(p)$, nor even that $p$ be in the domain of $f$.

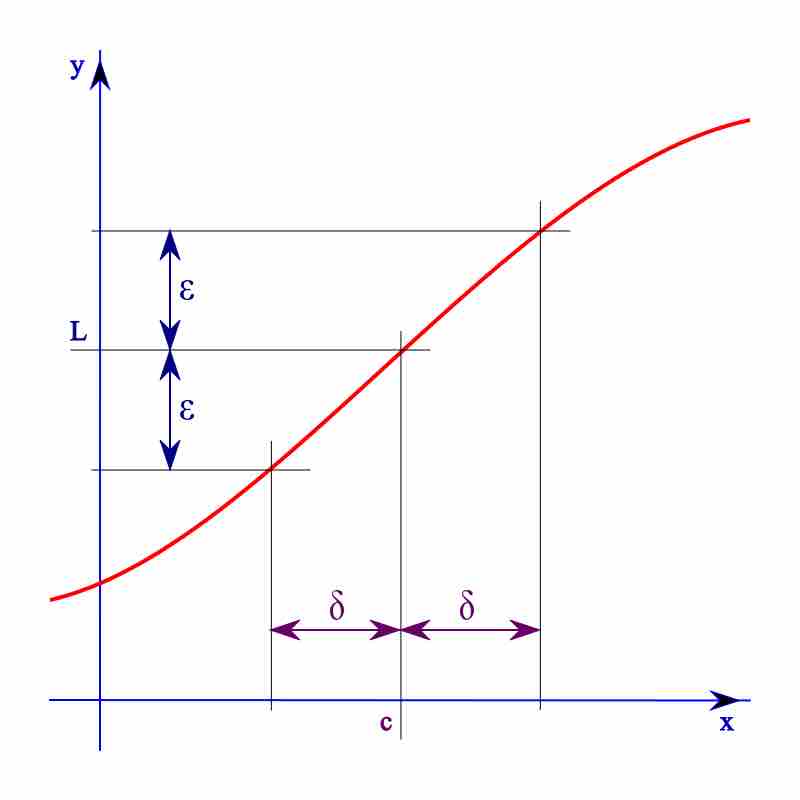
Definitely of a Limit

Whenever a point $x$ is within $\delta$ units of $c$, $f(x)$ is within $\epsilon$ units of $L$.

Example

For an arbitrarily small $\varepsilon$, there always exists a large enough number $N$ such that when $x$ approaches $N$, $\left | f(x)-L \right | < \varepsilon$. Therefore, the limit of this function at infinity exists.

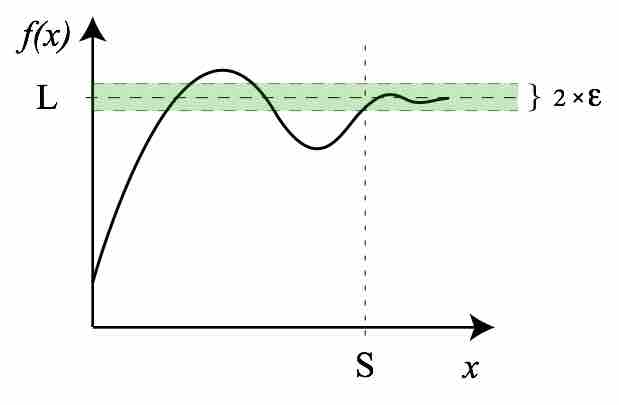
Limit of a Function at Infinity

For an arbitrarily small $\epsilon$, there always exists a large enough number $N$ such that when $x$ approaches $N$, $\left | f(x)-L \right | < \varepsilon$. Therefore, the limit of this function at infinity exists.

The letters $\varepsilon$ and $\delta$ can be understood as "error" and "distance," and in fact Cauchy used $\epsilon$ as an abbreviation for "error" in some of his work. In these terms, the error $(\varepsilon)$ in the measurement of the value at the limit can be made as small as desired by reducing the distance $(\delta)$ to the limit point.

This definition also works for functions with more than one input value. In those cases, $\delta$ can be understood as the radius of a circle or sphere or higher-dimensional analogy, in the domain of the function and centered at the point where the existence of a limit is being proven, for which every point inside produces a function value less than ε from the value of the function at the limit point.