Functions

In mathematics, a function is a relation between a set of inputs and a set of permissible outputs. Functions have the property that each input is related to exactly one output. For example, in the function $f(x)=x^2$ any input for $x$ will give one output only.

Functions are typically named with a single letter, like $f$. $f(x)$ is read "$f$ of $x$", and represents the output of the function $f$ corresponding to an input $x$. The input variable(s) are sometimes referred to as the argument(s) of the function. Consider the following example:

Let $f(x)=x^2$

Let $x=-3$, then:

$\displaystyle f(-3)=(-3)^2 $

$\displaystyle =9$

In the example above, the argument is $x=-3$ and the output is $9$. We write the function as:$f(-3)=9$. 

In the case of a function with just one input variable, the input and output of the function can be expressed as an ordered pair. The order is such that the first element is the argument and the second is the output. In the example above, $f(x)=x^2$, we have the ordered pair $(−3, 9)$. If both the input and output are real numbers then the ordered pair can be viewed as the Cartesian coordinates of a point on the graph of the function.

Another commonly used notation for a function is $f:X\rightarrow Y$, which reads as saying that $f$ is a function that maps values from the set $X$ onto values of the set $Y$.

Functions as a Machine

Functions are often described as a machine in a box that is open on two ends. You put something into one end of the box, it gets changed inside of the box, and then the result pops out the other end. The function is the machine inside the box and it's defined by what it does to whatever you put into it.

Function Machine

A function $f$ takes an input $x$ and returns an output $f(x)$. One metaphor describes the function as a "machine", that for each input returns a corresponding output.

Let's say the machine has a blade that slices whatever you put in into two and sends one half of that object out the other end. If you put in a banana you would get back half a banana. If you put in an apple you would get back half an apple.

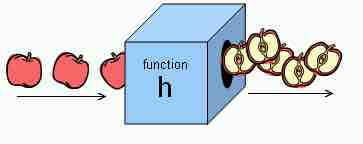
Fruit Halving Function

This shows a function that takes a fruit as input and releases half the fruit as output.

Let's define the function to take what you put into it and cut it in half. That is, the function divides the input by two. If you put in $2$ you would get back $1$. If you put in $57$ you would get back $28.5$. The function machine allows us to alter expressions. In this example, the function would be written as: 

$\displaystyle f(x)=\frac{1}{2}x$.

Functions As a Relation

Functions can also be thought of as a subset of relations. A relation is a connection between values in one set and values in another. In other words, each number you put in is associated with each number you get out. In a function every input number is associated with exactly one output number In a relation an input number may be associated with multiple or no output numbers. This is an important fact about functions that cannot be stressed enough: every possible input to the function must have one and only one output. All functions are relations, but not all relations are functions.