Equations and Inequalities

Equations

An equation is a mathematical statement that asserts the equality of two expressions. This is written by placing the expressions on either side of an equals sign (=), for example:

$x + 3 = 5$

asserts that $x+3$ is equal to $5$.

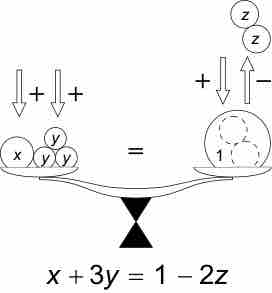
Equation as a Balance

Illustration of a simple equation as a balance. $x$, $y$, and $z$ are real numbers, analogous to weights.

Equations often express relationships between given quantities—the knowns—and quantities yet to be determined—the unknowns. By convention, unknowns are denoted by letters at the end of the alphabet ($x$, $y$, $z$, $\cdots$), while knowns are denoted by letters at the beginning ($a$, $b$, $c$, $\cdots$) . The process of expressing the unknowns in terms of the knowns is called solving the equation. In an equation with a single unknown, a value of that unknown for which the equation is true is called a solution or root of the equation. In a set of simultaneous equations, or system of equations, multiple equations are given with multiple unknowns. A solution to the system is an assignment of values to all the unknowns so that all of the equations are true.

Inequalities

An inequality is a relation that holds between two values when they are different. The notation $a \neq b$ means that a is not equal to $b$. It does not say that one is greater than the other, or even that they can be compared in size.

In either case, $a$ is not equal to $b$. These relations are known as strict inequalities. To compare the size of the values, there are two types of relations:

• The notation $a < b$ means that a is less than $b$. (It may also be read as "a is strictly less than $b$".)
• The notation $a > b$ means that a is greater than $b$.

In contrast to strict inequalities, there are two types of inequality relations that are not strict:

• The notation $a \leq b$ means that $a$ is less than or equal to $b$ (or, equivalently, not greater than $b$, or at most $b$).
• The notation $a \geq b$ means that $a$ is greater than or equal to $b$ (or, equivalently, not less than $b$, or at least $b$).