Quadratic relationships between variables are commonly found in physical sciences, engineering, and elsewhere. Perhaps the most universally used example of quadratic relationships in problem solving concerns right triangles.
The Pythagorean Theorem
The Pythagorean Theorem is used to relate the three sides of right triangles. It states:
This says that the square of the length of the hypotenuse (
In practice, the Pythagorean Theorem is often solved via factoring or completing the square. If any of the variables
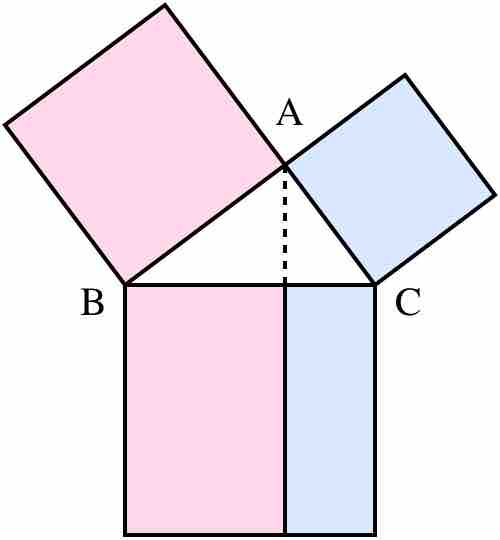
Euclid's Proof of the Pythagorean Theorem
Euclid used this diagram to explain how the sum of the squares of the triangle's smaller sides (pink and blue) sum to equal the area of the square of the hypotenuse.
Gravity and Projectile Motion
Most all equations involving gravity include a second-order relationship.
Gravitational Force
Consider the equation relating gravitational force (
The shape of this function is not a parabola, but becomes such a shape if rearranged to solve for
The general form of this function is:
which you should recognize as the vertex form of a quadratic equation.
Projectile Motion
The maximum height of a projectile launched directly upwards can also be calculated from a quadratic relationship. The formula relates height (
The same maximum height of a projectile launched directly upwards can be found using the time at the projectile's peak (
Substituting any time (
Electrostatic Force
The equation relating electrostatic force (
This is known as Coulomb's Law. Solving for either charge results in a quadratic equation where the charge is dependent on