Mathematical Models
A mathematical model is a description of a system using mathematical concepts and language. Mathematical models are used not only in the natural sciences and engineering disciplines, but also in the social sciences. Linear modeling can include population change, telephone call charges, the cost of renting a bike, weight management, or fundraising. A linear model includes the rate of change
Real Life Linear Model
Many everyday activities require the use of mathematical models, perhaps unconsciously. One difficulty with mathematical models lies in translating the real world application into an accurate mathematical representation.
Example: Renting a Moving Van
A rental company charges a flat fee of
Using the slope-intercept form of a linear equation, with the total cost labeled
The total cost is equal to the rate per mile times the number of miles driven plus the cost for the flat fee:
To calculate the cost of a
Real life Model with Multiple Equations
It's also possible to model multiple lines and their equations.
Example
Initially, trains A and B are
First, begin with the starting positions of the trains, (
Second, in order to write the equations representing each train's total distance in terms of time, calculate the rate of change for each train. Since train A is traveling towards train B, which has a greater
The two lines are thus:
And:
The two trains will meet where the two lines intersect. To find where the two lines intersect set the equations equal to each other and solve for
Solving for
The two trains meet after
Plugging it into the first equation gives us
Here is the distance versus time graphic model of the two trains:
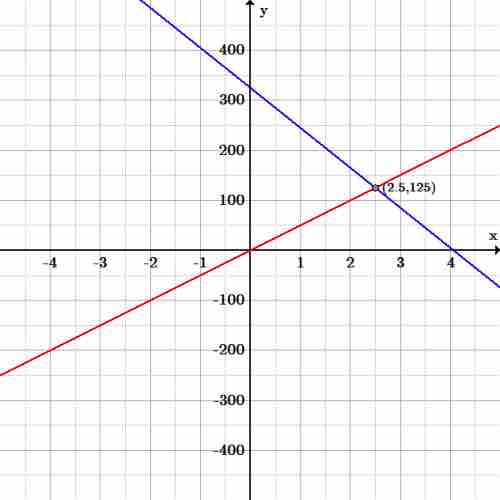
Trains
Train A (red line) is represented by the equation: