Absolute value is one of the simplest functions—and paradoxically, one of the most problematic. At face value, nothing could be simpler: absolute value simply means the distance a number is from zero. The absolute value of
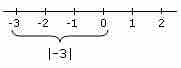
The following number line also illustrates this definition:
Absolute value
The absolute value of a real number may be thought of as its distance from zero. In this image, for example,
Types of Solutions to Absolute Value Equations
Consider the following three equations. They look very similar—only the number changes—but the solutions are completely different. These three equations demonstrate how absolute value equations can have one, two, or no solutions.
Equation 1
What value(s) will make this equation true?
Equation 2
Here, neither
Equation 3
What value(s) will make this equation true?
Solving Absolute Value Equations
The following steps describe how to solve an absolute value equation:
- Isolate the absolute value term algebraically.
- Set up two separate equations: For the first, keep the new equation you found in step 1, but remove the absolute value signs; for the second, keep the equation you found in step 1, remove the absolute value signs, and multiply one side by -1.
- Solve the pair of equations.
For example, let's solve the following equation for
Step 1
First, algebraically isolate the absolute value by adding 7 to both sides of equation and then dividing both sides by 3:
Step 2
Now, set up two separate equations. The first is the equation we found in Step 1, but with the absolute value signs removed:
The second equation is the one we found in Step 1, with the absolute value signs removed, and with the other side multiplied by -1:
Step 3
Now, solve both equations. For the first:
For the second equation:
Therefore, this problem has two answers: