Why Use a Logarithmic Scale?
Many mathematical and physical relationships are functionally dependent on high-order variables. This means that for small changes in the independent variable there are very large changes in the dependent variable. Thus, it becomes difficult to graph such functions on the standard axis.
Consider, as an example, the Stefan-Boltzmann law, which relates the power (j*) emitted by a black body to temperature (T).
On a standard graph, this equation can be quite unwieldy. The fourth-degree dependence on temperature means that power increases extremely quickly. The fact that the rate is ever-increasing (and steeply so) means that changing scale (scaling the axes by
For very steep functions, it is possible to plot points more smoothly while retaining the integrity of the data: one can use a graph with a logarithmic scale . Here are some examples of functions graphed on a linear scale, semi-log and logarithmic scales.
The top left is a linear scale. The bottom right is a logarithmic scale. The top right and bottom left are called semi-log scales because one axis is scaled linearly while the other is scaled using logarithms.
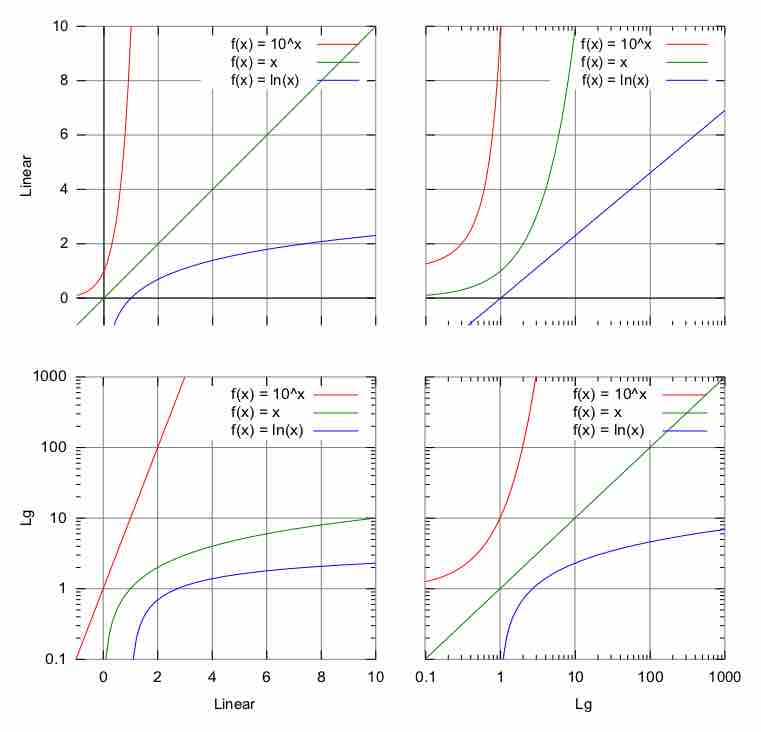
Logarithmic scale
The graphs of functions
As you can see, when both axis used a logarithmic scale (bottom right) the graph retained the properties of the original graph (top left) where both axis were scaled using a linear scale. That means that if we want to graph a function that is unwieldy on a linear scale we can use a logarithmic scale on each axis and retain the properties of the graph while at the same time making it easier to graph.
It should be noted that the examples in the graphs were meant to illustrate a point and that the functions graphed were not necessarily unwieldy on a linearly scales set of axes.
Converting Linear to Logarithmic Scales
The primary difference between the logarithmic and linear scales is that, while the difference in value between linear points of equal distance remains constant (that is, if the space from
Thus, if one wanted to convert a linear scale (with values
The advantages of using a logarithmic scale are twofold. Firstly, doing so allows one to plot a very large range of data without losing the shape of the graph. Secondly, it allows one to interpolate at any point on the plot, regardless of the range of the graph. Similar data plotted on a linear scale is less clear.
Solving Problems Using Logarithmic Graphs
A key point about using logarithmic graphs to solve problems is that they expand scales to the point at which large ranges of data make more sense. In the equation mentioned above (
Taking the logarithm of each side of the equations yields:
Recall the following properties of logarithms:
Using the above, our equation becomes: