A system of inequalities consists of two or more inequalities, which are statements that one quantity is greater than or less than another. A nonlinear inequality is an inequality that involves a nonlinear expression—a polynomial function of degree 2 or higher. The most common way of solving one inequality with two variables
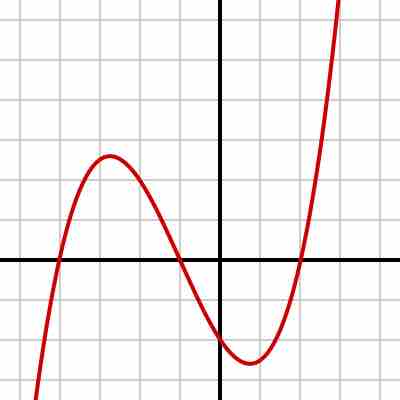
Cubic function
This graph of a cubic function is an example of a nonlinear equation.
Every inequality has a boundary line, which is the equation produced by changing the inequality relation to an equals sign.
The boundary line is drawn as a dashed line (if
Consider, for example, the system including the parabolic nonlinear inequality:
and the linear inequality:
All points below the line
Graphing both inequalities reveals one region of overlap: the area where the parabola dips below the line. This area is the solution to the system.
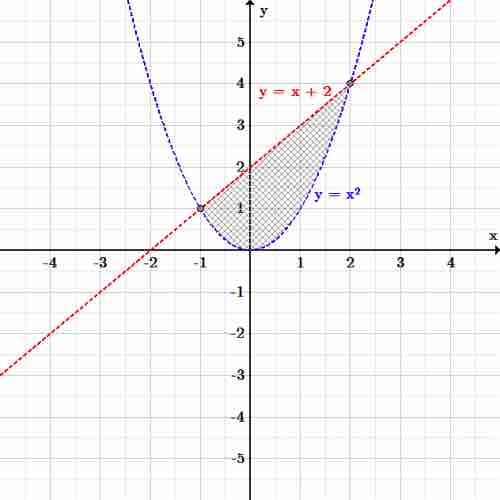
Nonlinear system of inequalities
Any point in the region between the line
The limits of each inequality intersect at
This need not be the case with all nonlinear inequalities, but reversing the direction of both inequalities in the previous example would lead to an infinite solution area.