Binomial Theorem

The binomial theorem is an algebraic method of expanding a binomial expression. Essentially, it demonstrates what happens when you multiply a binomial by itself (as many times as you want). For example, consider the expression $(4x+y)^7$. It would take quite a long time to multiply the binomial $(4x+y)$ out seven times. The binomial theorem provides a short cut, or a formula that yields the expanded form of this expression.

According to the theorem, it is possible to expand the power $(x+y)^n$ into a sum involving terms of the form $ax^by^c$, where the exponents $b$ and $c$ are nonnegative integers with $b+c=n$, and the coefficient $a$ of each term is a specific positive integer depending on $n$ and $b$. When an exponent is zero, the corresponding power is usually omitted from the term (so that $3x^2y^0$ would be written as $3x^2$).

For example, consider the following expansion:

$\displaystyle {(x+y)}^{4}={x}^{4}+4{x}^{3}{y}+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4}$

Any coefficient $a$ in a term $ax^by^c$ of the expanded version is known as a binomial coefficient. The binomial coefficient also arises in combinatorics, where it gives the number of different combinations of $b$ elements that can be chosen from a set of $n$ elements. Recall that this could be written with the notation $\begin{pmatrix} n \\ b \end{pmatrix}$, or "$n$ choose $b$."

According to the binomial theorem, it is possible to expand any power of $x + y$ into a sum of the form:

$\displaystyle { (x+y) }^{ n }=\begin{pmatrix} n \\ 0 \end{pmatrix}{ x }^{ n }{ y }^{ 0 }+\begin{pmatrix} n \\ 1 \end{pmatrix}{ x }^{ n-1 }{ y }^{ 1 } \\ +\begin{pmatrix} n \\ 2 \end{pmatrix}{ x }^{ n-2 }{ y }^{ 2 }+\dots +\begin{pmatrix} n \\ n-1 \end{pmatrix}{ x }^{ 1 }{ y }^{ n-1 }+\begin{pmatrix} n \\ n \end{pmatrix}{ x }^{ 0 }{ y }^{ n }$

where each value $\begin{pmatrix} n \\ k \end{pmatrix} $ is a specific positive integer known as binomial coefficient. This formula is referred to as the Binomial Formula. Using summation notation, it can be written as:

$\displaystyle { (x+y) }^{ n }=\sum _{ k=0 }^{ n }{ \begin{pmatrix} n \\ k \end{pmatrix} } { x }^{ n-k }{ y }^{ k }=\sum _{ k=0 }^{ n }{ \begin{pmatrix} n \\ k \end{pmatrix} } { x }^{ k }{ y }^{ n-k }$

A significant amount of time may be required to apply the binomial theorem and perform all of the calculations in the above formula, particularly for high values of $n$. Therefore, what follows is a shortcut for finding binomial expansions using a visual tool.

Pascal's Triangle

Pascal's triangle is an alternative way of determining the coefficients that arise in binomial expansions, using a diagram rather than algebraic methods. For a binomial expansion with a relatively small exponent, this can be a straightforward way to determine the coefficients. 

In the diagram below, notice that each number in the triangle is the sum of the two directly above it. This pattern continues indefinitely. 

Pascal's Triangle

Each number in the triangle is the sum of the two directly above it.

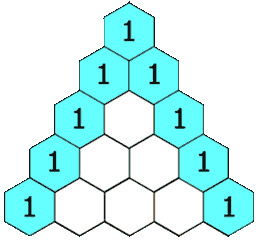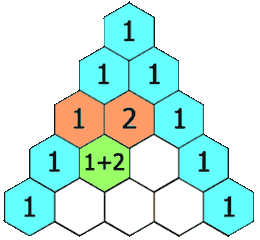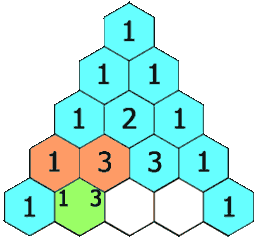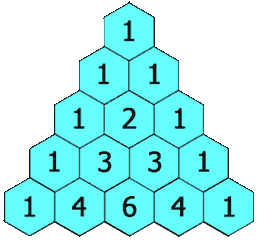
The rows of Pascal's triangle are numbered, starting with row $n = 0$ at the top. The entries in each row are numbered from the left beginning with $k = 0$ and are usually staggered relative to the numbers in the adjacent rows. A simple construction of the triangle proceeds in the following manner. On row $0$, write only the number $1$. Then, to construct the elements of following rows, add the two above numbers to find the new value. If either of the above numbers is not present, substitute a zero in its place. For example, each number in row one is $0 + 1 = 1$.

To understand how this pattern applies to the binomial formula, consider the expansion:

$\displaystyle {(x + y)}^{2} = {x}^{2} + 2xy + {y}^{2} = 1{x}^{2}{y}^{0} + 2{x}^{1}{y}^{1} + 1{x}^{0}{y}^{2}$

Notice the coefficients are the numbers in row two of Pascal's triangle: $1,2,1$. In general, when a binomial like $x+y$ is raised to a positive integer power we have:

$\displaystyle {(x + y)}^{n} = {a}_{0}{x}^{n} + {a}_{1}{x}^{n-1}y +{a}_{2}{x}^{n-2} {y}^{2} + \cdot\cdot\cdot {a}_{n-1}{x}{y}^{n-1} + {a}_{n}{y}^{n}$

Where the coefficients $a_i$ in this expansion are precisely the numbers on row $n$ of Pascal's triangle. 

Notice that the entire right diagonal of Pascal's triangle corresponds to the coefficient of $y^n$ in these binomial expansions, while the next diagonal corresponds to the coefficient of $xy^{n−1}$ and so on. 

Example: Find the expansion of $(x+y)^5$ using Pascal's triangle

Notice that $n=5$, and recall that this would correspond to row 5 of Pascal's triangle. 

Pascal's Triangle

Pascal's triangle with 5 rows. 

Recall that the binomial expansion of $(x+y)^5$ will be written in the following form, where the coefficients are the numbers in row $5$ of Pascal's triangle:

$\displaystyle {(x + y)}^{5} = {a}_{0}{x}^{5} + {a}_{1}{x}^{4}y +{a}_{2}{x}^{3} {y}^{2} + {a}_{3}{x}^2{y}^{3} + {a}_{4}{x}{y}^{4}+{a}_{5}{y}^{5}$

It can be observed in the triangle that row $5$ is $1, 5, 10, 10, 5, 1$. Applying these numbers to the binomial expansion, we have:

$\displaystyle {(x + y)}^{5} = {x}^{5} + 5{x}^{4}{y} + 10{x}^{3}{y}^{2} + 10{x}^{2}y^{3} + 5{x}{y}^{4} + {y}^{5} $