The time value of money framework says that money in the future is not worth as much as money in the present. Investors would prefer to have the money today because then they are able to spend it, save it, or invest it right now instead of having to wait to be able to use it.
The difference between what the money is worth today and what it will be worth at a point in the future can be quantified. The value of the money today is called the present value (PV), and the value of the money in the future is called the future value (FV). There is also a name for the cost of not having the money today: the interest rate or discount rate (i or r). For example, if the interest rate is 3% per year, it means that you would be willing to pay 3% of the money to have it one year sooner. The amount of time is also represented by a variable: the number of periods (n). One period could be any length of time, such as one day, one month, or one year, but it must be clearly defined, consistent with the time units in the interest rate, and constant throughout your calculations.
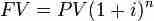
FV of a single payment
The FV is related to the PV by being i% more each period.
All of these variables are related through an equation that helps you find the PV of a single amount of money. That is, it tells you what a single payment is worth today, but not what a series of payments is worth today (that will come later). relates all of the variables together. In order to find the PV, you must know the FV, i, and n.
When considering a single-period investment, n is, by definition, one. That means that the PV is simply FV divided by 1+i. There is a cost to not having the money for one year, which is what the interest rate represents. Therefore, the PV is i% less than the FV.