I'd be happy to explain my comments further :-)
Unfortunately it's not a simple explanation.
For a bcrypt-hashed password, how much of an advantage would this give the attacker? Can this be quantified?
Quantifying this will be hard since guessing at the runtime of an algorithm is tough, especially if the attacker is allowed to make specialized chips for the job.
So no fancy math :-( but I can still give an intuition-based answer;
bcrypt is designed for hashing passwords in a way which is robust to offline dictionary attacks, meaning that, among other things, it is slow. Slow means that an attacker who is brute-forcing has to do more computations per guess, and therefore can't make as many guesses per second. Or, in economic terms, the amount of money that an attacker has to spend on processors and electricity in order to crack your password skyrockets when you use a nice slow hash function.
To illustrate the point, this table, taken from a paper by Colin Percival (full reference below), shows the estimated cost of hardware you'd need in order to reliably crack a hash in a year (note that this is the cost for the number of 2002-era processors you'd need, it completely ignores the costs of electricity, power supplies, cooling, etc).
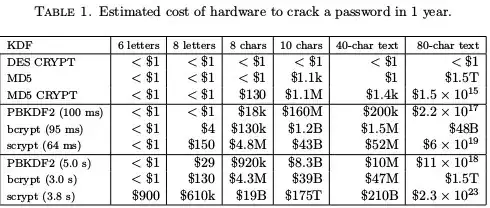
Now that we've established that slow is good, and that good hash functions are slow, let's talk about zxcvbn.
zxcvbn is meant to be a javascript dohicky that runs client-side without lagging up the page, so compared to PBKDF2, bcrypt, and scrypt, it is lightening fast.
To actually answer your question, imagine that I stole a password database where each row looked like this (which is what I believe @ScottArciszewski was describing in his comment here):
username bcrypt_hash bgcypt_salt zxcvbn_score
happyfish23 IjZAgcfl7p92ldGxad68LJZdL17lhWy N9qo8uLOickgx2ZMRZoMye 32.827
Typically a brute-force attack will take a password from its dictionary, hash it, and see if the hash matches the one in the stolen database, if it does then I've cracked your password, otherwise I keep trying until I find one that does match. (This can either be done online one-at-a-time as passwords are guessed, or as a pre-computed rainbow table, but either way, slowing this down costs time and money, esp. since you need a different rainbow table for each alg + iteration_count salt combination)
With access to the above database, I could use the zxcvbn score as a filter; if the zxcvbn scores don't match, then I already know that it's not the right password and there's no point wasting time on the bcrypt calculation. So I only need to compute bcrypt if zxcvbn matches. Since zxcvbn is basically free, compared to bcrypt, it's not unreasonable that a brute-forcer could go from 10 guesses / second to millions of guesses / second using this trick.
As for the second part of your question:
Also, other comments mention that reducing the precision of the entropy reduces the attacker's advantage. Would storing only the score (0, 1, 2, 3, or 4) effectively eliminate the advantage?
Yes, this would effectively eliminate the advantage. The reason why basically falls out of the explanation above. Let's assume that the original database stores a 5-digit zxcvbn score, and that passwords in the brute-forcing dictionary are uniformly distributed over zxcvbn scores (a terrible assumption, but it makes the logic easy). You would only expect the zxcvbn scores to match 1 / 100,000th of the time, so you only have to compute a bcrypt for every 100,000th guess. But if instead you store a lower-precision version of the score, for example {0,1,2,3,4}, then you'd be forced to compute bcrypt for every 5th guess. You're still giving the attacker a ~5x speedup, but that's WAAAYY better than a 100,000x speedup.
REFERENCE:
Percival, Colin. "Stronger key derivation via sequential memory-hard functions." Self-published (2009): p. 14 (link to pdf)
