How many combinations does a specific password policy allow?

Question

Recently I was arguing about password policies. Assume you have a policy which requires 10 characters and additionally at least one letter, one number and one special character. My companion was arguing that this policy is weaker than one that requires at least 10 characters. While this is computationally true, we couldn't agree how many combinations the first policy allows. How many combinations does the first policy have and is it really much less than the second policy?

Answer 1

Your companion is right that the least restrictive policy has a higher potential entropy, as it can encode a larger amount of information. This being said, the entropy of a set of data depends on the probability distribution of each datum appearing in the dataset. Therefore, the quality of a password policy should not be measured in terms of how much information can be encoded, but in terms of how much it prevents different users from using similar passwords.

Simply throwing in mandatory numbers does very little for that purpose, and a site that randomly assigns 7-character long passwords composed of numbers, symbols and letters would probably achieve a higher overall entropy. It's impossible to give an authoritative answer as to whether there is a significant difference of quality between the two proposed policies because:

• they both require higher amounts of user memory than most passwords observed in the wild require, meaning neither is likely to have significantly higher amounts of weak password reuse
• none of these models is common enough for any public/leaked password dataset to be available for reasoning about probability distributions
• there is no generative model of human password choices that could explain how actual humans would make passwords on these sites¹

¹ some might claim they have such a model - given the superficiality of state of the art research on human password choices, this is very unlikely. The latest research only addresses behaviours with regard to a unique credential, with populations that are unrealistically motivated in authenticating to studied services (because of how password behaviour experiments are constructed). Current research is also strongly culturally biased towards US/UK individuals as demonstrated by Li et al. 2014. Until these limitations are addressed and much more data is collected

If you want to understand how to estimate the strength of an individual password the current method to apply would be to implement Bonneau's password strength metrics.

Answer 2

This has had some good pointers to password strength, so the OP's question is probably not important. I think dexgecko had it right, but was hard to read. So in the interest of answering questions as simply as possible:

Let X = { ten character passwords }
Let A = { ten character passwords with no letters }
Let B = { ten character passwords with no numbers }
Let C = { ten character passwords with no special characters }

(I'm using + for set unions, and * for set intersections.)

The first policy forbids A + B + C, so the size of the first policy is

| X \ (A + B + C) | = | X | - | A + B + C |

Now |X| is kind of trivial, as noted. The size of a union can be computed by Principle of Inclusion/Exclusion

| A + B + C | = |A| + |B| + |C| - (|A * B| + |B * C| + |A * C|) + (|A * B * C|)

These are actually pretty easy to count. The size of A is that of passwords with no letters, i.e. just numbers and special characters. The size of B and C are similar. The size of A * B is that of passwords with no letters or numbers, i.e. just special characters. The size of A * B * C is that of passwords with no symbols, i.e. empty.

So the size of the forbidden passwords is

(10+33)^10 + (52+33)^10 + (52+10)^10 - (33^10 + 52^10 + 10^10)

which is what dexgecko came up with.

So perhaps the surprising point is that if you have a password manager that ensures all elements of that 10 character keyspace are equally probable, there is about one chance in three that you will have to discard the first thing it chooses.

I'd argue that we are long past the time of human generated passwords. :-(

Answer 3

So I'm going to try and answer how many combinations actually exist for each policy. Please post a comment if you feel the logic is flawed.

First we look at the number of characters available when including each of numbers (N), letters (L) and specials (S).

• N - 10
• L - 52
• S - 33
• LS - 85
• NS - 43

• NL - 62

• NLS - 95

---

EDIT :

For the first policy, we remove from the total the combinations for each individual character set and the paired up sets (which have the individual combinations removed from themselves).

Policy 1

= NLS - N - L - S - (LS - L - S) - (NS - N - S) - (NL - N - L)

= 95^x - 85^x - 43^x - 62^x + 10^x + 52^x + 33^x

Policy 2

= NLS

= 95^x

At 10 characters, Policy 1 is at approximately 65.92% of Policy 2. At 20 characters Policy 1 is around 89.17% of Policy 2.

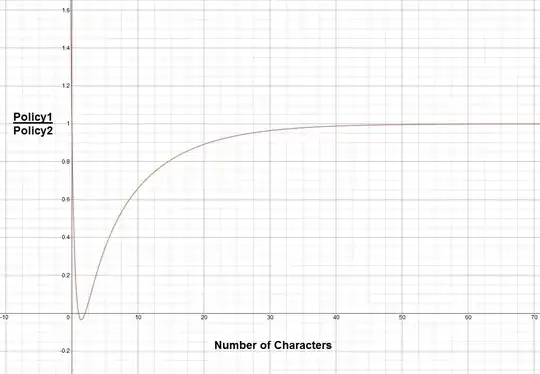Credits: Desmos

Answer 4

My companion was arguing that this policy is weaker than one that requires at least 10 characters.

A password policy is designed to prevent "weak" passwords (more on what this actually means below), therefore it has to be judged on the weakest password that can be created under it, not by the number of passwords that can possibly be encoded with it.

Say we have 52 letters (upper and lower), 10 digits and 30 other characters.

The weakest password generation method possible with 10 characters and at least one of each character type would be 8 numbers (as there are only 10 digits in the entropy pool it is the lowest available of the character types) and one each of a letter and a symbol. Say 12345678A@.

Calculating the entropy pool of such a password generated in this manner gives

2^(log2(10) * 8 + log2(52) + log2(30)) = 156,000,000,000 permutations.

The weakest password possible with 10 characters would be 10 characters from the type of character with the lowest entropy pool - numbers only. Say 1234567890.

2^(log2(10) * 10) = 10,000,000,000 possible combinations from this entropy pool.

_{Calculations shown for entropy calculation for purpose of explanation, however you could just multiply them together to get the same result: e.g. 10^8 * 52 * 30 = 156,000,000,000}

So

     156,000,000,000 vs
      10,000,000,000 vs

Therefore the first policy enforces a "stronger" password. Remember that password strength is not a real metric, only entropy counts and that is based on how the password is generated. So if the password was basketball it would be cracked immediately using the second policy.

Additionally with the first policy, the number and the symbol can appear anywhere, not just at the start, increasing the number of permutations. Remember though we're going for the weakest possible password, so if a user was to be forced to have a letter and a number they are likely to stick them at the end (and in that order).

If you want to calculate it, multiply by the number of permutations (times 10 for positions of the number and times 9 for the positions of the symbol, as the symbol cannot appear in the same position as the number, however either way is fine).

156,000,000,000 * 10 * 9 = 14,040,000,000,000

For completeness, to get the maximum number of permutations the calculations would be as follows, assuming 10 characters is the maximum limit too, otherwise it'd be an impossible question to answer. Note that here we are using the full entropy pool as we are going for the most "complex" password possible. Say Azz643@$%2 - as even as you can get spread of each character type.

52^8 * 10 * 30 * 10 * 9 = 1,443,412,670,349,312,000
92^10 = 43,438,845,422,363,213,824

So here we have

 1,443,412,670,349,312,000 vs
43,438,845,422,363,213,824

This gives you 60 bits vs 65 bits of entropy.

So yes, there are way more combinations possible that can be encoded using the second policy, but in real terms you may get lots of basketballs.

Answer 5

The specific-conditional entropy can be greater than the entropy.

This is the key mathematical fact. You are arguing about the number of combinations but you should be arguing about entropy. These kinds of password policies only make sense if the user picks the password and is not uniformly generated.

In these cases, by restricting the possible pool of values (passwords), we may get something that has higher entropy than the original. This is a mathematical fact, the entropy can be increased.

To illustrate this on an exaggerated example, imagine a random variable X, with potential values 1, 2 and 3, and corresponding probabilities 98%, 1%, 1%, respectively. Let's calculate what happens if we disallow the value 1.

• The original entropy of X is H(X) = 0.16 bits.
• However conditionally: H(X | X=2 or X=3) = 1 bit.

By disallowing the obvious and very high probability value, we got a uniform 50%-50% distribution and a higher resulting entropy.

Something similar is going on with passwords. Users tend to have a preference for a specific set of passwords (like X=1 in the example), but outside of that set, they probably don't have strong preferences (like X=2 and X=3 have equal probabilities). So by forcing them to not use the preferred ones, they must go to a territory where they will pick more unpredictably. By requiring special characters, we disallow the highly probable set of passwords that have no such special characters. (Most people wouldn't think of including them naturally.)

In practice, it still doesn't result in a uniform distribution of course. The typical choice will still be an originally preferred password with some twist on it (some special characters here and there). But that twist is quite random and greatly increases the final entropy... Well, unless the twist is predictable because it's just a l33t-ification (switching 0 for o, $ for s, etc.), in which case it's just a slight increase.

This does not mean that such password policies are really the way to go, since psychological factors are also important to consider (and actually, password managers with random passwords seem to be the best solution in most cases).

Nevertheless, mathematically, such a restriction may indeed make passwords stronger.