How is the strength of a key/Password determined

Question

I was reading about the Principle of Key Sizes and came across this table:

The deduction I made off this is that after a certain key size, increase in a single bit causes Time required for search to get doubled from the previous one.

Then, I came across this video How to crack Passwords in which Prof. Pound tell's that your key strength is somewhat related to the character set of your password/Key.

For Instance if my password is of 8 length and its character set is lowercase characters, then total attempts required to crack my password will be 26^8 = 208827064576 (character_set ^ keysize) (on the worst case).

So I was wondering, whether the increase in Key_Size by bits, and this character set theory is somewhat related or not. If yes, then why most people measure strength of key by the number of bits it has, rather then the character set it uses?

And what is the most common character set used in password/key cracking, as most character tables (ASCII/UTF8) contains a lot of NPC's and/or Emoji's etc. so are they excluded during the key search process or not?

Answer 1

I think you might be confusing "size/length" with "entropy". The text string 123456, when encoded in either UTF8 or other common encodings (ISO-8859-1 or "Latin", etc.), will be 8 x 6 = 48 bits in length. However, its entropy will be... ridiculous. I can't even estimate it, all I know is that any script kiddie will definitely be able to attack you successfully with such a weak password. The "size/length" in bits is related to the encoding using for the text. The "entropy" on the other hand is related to the randomness, or in other words the number of possible combinations that an attacker will have to try to be able to guess it.

A key is just a series of bits: 011001100010101011101... In a 128-bit key of course there are 128 bits. If those bits are truly random, then you will have an extremely strong key, containing 128 bits of entropy. But in reality keys are often (but not always and not necessarily) generated starting from a password or passphrase, because people will need to remember them. How can you remember 128 bits easily? That's impossible.

So people will just pick a password, and then an algorithm called "key derivation function" will transform the password into a key (a series of random bits). So what happens is that an attacker won't try to bruteforce the generated password, because they know that it's impossible to bruteforce 128 random bits in a reasonable time. So what the attacker does is try to bruteforce your password, generate the related key for each password, and try. Your password is very likely to contain much less than 128 bits of entropy, that's why the attacker will try to bruteforce the password instead of the key. For example, a 12-character password containing random uppercase/lowercase characters and numbers is going to have 62^12 = 3.23 x 10^21 = about 2^71 = about 71 bits of entropy.

Attackers usually have dictionaries and are going to bruteforce passwords using the most common words and patterns, rather than trying all the possible combinations at random. So for example they might try abc123, dogcatbird11, 5tr0ngPa55w0rd, etc. They might try to include some common symbols in the possible character set, for example question marks, exclamation marks, etc. but leave out other less common characters. In the end, it all depends on how much time and resources the attacker is willing to waste. Bruteforcing all the possible 8-character passwords might be feasible, but as soon as the complexity increases the attacker will have to make some specific choices, unless they feel like waiting for centuries in front of their computer.

Answer 2

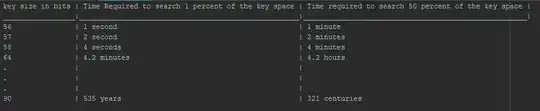
The deduction I made off this is that after a certain key size, increase in a single bit causes Time required for search to get doubled from the previous one.

Not just after a certain key size, that's how it works in general. Assuming a random key, if it's 8 bits there will be 2⁸ possible keys, and it will take about 2⁷ = 128 tries on average to guess it (on average you'll guess it after searching about half the keyspace). Each additional bit in the key doubles the keyspace, and thus doubles the expected time to guess the correct key.

For Instance If My password is of 8 length and its character set is lowercase characters, then total attempts required to crack my password will be 26^8 = 208827064576 (character_set ^ keysize) (on the worst case).

So I was wondering, whether the increase in Key_Size by bits, and this character set theory is somewhat related or not.

Yes, this is the same idea. If you break a key into bytes (sets of 8 bits), then each byte added multiplies the keyspace by 2⁸ = 256. For random lowercase passwords, each character added multiplies the password space by 26 (or about 2^4.7).

If yes, then why most people measure strength of key by the number of bits it has, rather then the character set it uses?

Because keys aren't related to character sets. Keys are random binary. You can represent them as 0s and 1s, or as hexadecimal, or any number of other ways, but what matters is the keyspace, which is directly related to the key length in bits.

And what is the most common character set used in password/key cracking, as most character tables (ASCII/UTF8) contains a lot of NPC's and/or Emoji's etc. so are they excluded during the key search process or not?

That depends on the password cracking tool and configuration being used, though printable ASCII is common given that most passwords are ASCII. Many password cracking tools also prioritize common patterns and mutations of previously cracked passwords. Passwords are generally crackable only because they are chosen poorly.

Keys generally aren't attacked directly, as 128 bit keys are impossible to brute-force. An old 64 bit key might be brute-forced directly, in which case there's not really a character set used per se, it's just iterating all possible sequences of 64 bits.

Answer 3

This is confusing because keys don't use UTF8 or ASCII. The reason keys strength is shown in bits is because they are generally hexadecimal (or binary expressed as hexadecimal) data types. A hexadecimal key only contains 16 characters (0-9,A-F). One character per 4 bits. Because these are all useable values, there are no weird characters like ♥ or ╟ to be excluded. As such a 128-bit key is actually 32-characters vs the 16-characters you would see in UTF8 or ASCII password of equivalent bit-strength.

Passwords normally use 8-bit character sets instead because people want to type the fewest number of characters possible for the most complexity. Because people think in terms of characters, not bits, a password strength is evaluated by easily typed characters (0-9,a-z,A-Z,!@#$%^&*()-_=+{}[]:;"'<>,.?/~`) = 92. Even though 92 is a lot less than the 256 that are technically available, it's still much bigger that the 16 in a hex character set.

Keys are stored values that you never need to type in; so, a good bit-density is better than a good character density.